|
�y�I�[���̖@���z
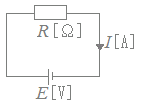
���d�r�̒��ɂ͓�����R������C������Rr[��]�������ł��Ȃ��傫���̂Ƃ��́CR+r[��]���S�̂̒�R�ɂȂ�܂��D�@�E�}�P�̂悤�ȉ�H�𗬂��d���̋���I[A]�͓d��E[V]�ɔ�Ⴕ�C��RR[��]�ɔ���Ⴕ�܂��D �@������I�[���̖@���Ƃ����܂��D I=…(1) �������E��\�����Ƃ��Ă��悭�g���܂��D E=IR…(2) �܂��C�d���Ɠd�������R�����߂鎮�Ƃ��Ă��g���܂��D R=…(3) I=…(1’) �@���ۂ̖��������Ƃ��ɁC������R�������ł��邩�ǂ����͖�������Ε�����܂��D |
�}�P
 ���ʏ�C�d����������Γd���������Ƃ����悤�ɍl���邱�Ƃ������ł����C�K���������̂悤�ɍl����K�v�͂Ȃ��C���̐}�̂悤�ȏꍇ�C��R�ɂ�IR=12[V]�̓d�����������Ă���ƌ����܂��D 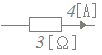 |
|
�m���n
�}�̂悤�ɁC������Rr[��]�C�N�d��E[V]�̓d�r�ɒ�RR[��]�̉ϒ�R���ڑ�������H������BR=2.25[��]�ɂ����Ƃ��C��H�𗬂��d����I=3[A]�ł������B���ɁCR=3.45[��]�ɂ����Ƃ��C��H�𗬂��d����I=2[A]�ƂȂ����B���̓d�r�̋N�d��E[V]�̒l�Ƃ��āC�������͎̂��̂����ǂꂩ�B 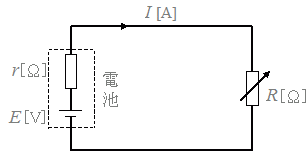 (1) 6.75 (2) 6.90 (3) 7.05 (4) 7.20 (5) 9.30 HELP ���p���F�d���O��@����18�N�x�u���_�v��5
|
r, E�𖢒m���Ƃ���A���������𗧂Ă�D
R=2.25�̂Ƃ��CI=3������ E=3(2.25+r)…(1)
R=3.45�̂Ƃ��CI=2������E=2(3.45+r)…(2)
(1)−(2)�ɂ��E�����������6.75+3r=6.9+2r
r=0.15
r=0.15��(1)�ɑ��E=3(2.25+0.15)=7.2→�y���z(4)
�y�������|�C���g�z
�@��R��R�C�d�r�̓�����R��r�̂Ƃ��C��H�ɂ͂����̒���ڑ��Ƃ���R+r�̒�R�����邱�ƂɂȂ�B |
|
�y��R�̒���ڑ��E����ڑ��ƍ�����R�z
�y����z�@���}�Q�̂悤�ɒ�R���e�XR1[��]�CR2[��]�̂Q�̒�R��ɂȂ����Ƃ��C������R�i�_���̕������P�̒�R�ɒu���������ꍇ�̒l�j�� R=R1+R2…(1) �@�E�}�R�̂悤�ɒ�R���e�XR1[��]�CR2[��]�̂Q�̒�R�����ɂȂ����Ƃ��C������R�i�_���̕������P�̒�R�ɒu���������ꍇ�̒l�j�� R=…(2)…�@�m�a�n���́m�ρn
�L���q�z�t�̖@�����g���܂����C����ɂ��Ă͌�ŏڂ����q�ׂ܂��D
�}�Q
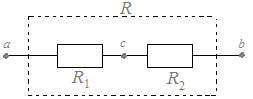
�@�}�Q�ɂ�����a,c�Ԃ�c,b�Ԃ𗬂��d���͋��ʂŁC�����I�Ƃ����ƁC
�@a,c�Ԃ̓d���Cc,b�Ԃ̓d���͊e�X IR1�CIR2 �@  a,b�Ԃ̓d��V�͂����̘a�ɓ��������� a,b�Ԃ̓d��V�͂����̘a�ɓ���������V=IR1+IR2=I(R1+R2) �ɂȂ�܂��D �@���������āC��R�� R==R1+R2 �ɂȂ�܂��D
�@��ʂɁC�������̒�RR1�CR2�CR3�C···��ڑ������Ƃ��̍�����R��
R1+R2+R3+··· �ɂȂ�܂��D �y��z �@�E�}�S�̂悤�ɒ���ڑ��ƕ���ڑ����g�ݍ��킳��Ă���Ƃ� �@R2�CR3�̕���ڑ��ɂ�鍇����R�� �@���̌��ʂ�R1�Ƃ̒���ڑ��ɂ��C�S�̂̍�����R�� R1+ |
�}�R
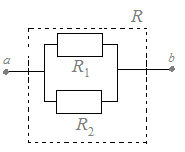
�@�}�R�ɂ�����a,b�Ԃ̓d����V�Ƃ����ƁC��RR1�CR2�ɗ����d���͊e�X
�C �@  a,b�Ԃ̓d��I�͂����̘a�ɓ��������� a,b�Ԃ̓d��I�͂����̘a�ɓ���������I=+=V(+) �ɂȂ�܂��D �@���������āC��R�� =+ �����܂��D �@�����ό`����ƁC R=…�@�m�a�n���́m�ρn
�@��ʂɁC�������̒�RR1�CR2�CR3�C···�����ڑ������Ƃ��̍�����R��
=+++··· �����܂��D �@�����ό`����ƁC R= ���R�ȏ�̏ꍇ�́C�m�a�n���́m�ρn�̂悤�ȊȒP�Ȓ������͂���܂���D �}�S 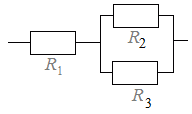 |
||
|
�m���P�n
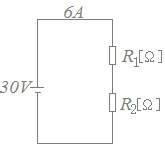
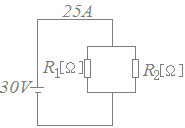
��R�l���قȂ��RR1[��]��R2[��]��}�P�̂悤�ɒ���ɐڑ����C30[V]�̒����d�����������Ƃ���C��H�ɗ����d����6[A]�ł������B ���ɁC���̒�RR1[��]��R2[��]��}�Q�̂悤�ɕ���ɐڑ����C30[V]�̒����d�����������Ƃ���C��H�ɗ����d����25[A]�ł������B���̂Ƃ��C��RR1[��]�CR2[��]�̂������������̒�R[��]�̒l�Ƃ��āC�����͎̂��̂����ǂꂩ�B
�@��ʍ��c�@�l�d�C�Z�p�Ҏ����Z���^�[���쐬�������
�@��O��d�C��C�Z�p�Ҏ����i�d���O��j����21�N�x�u���_�v��6 �@�Ȃ��C���y�щ���ɑ��鎿�ⓙ�́C�d�C�Z�p�Ҏ����Z���^�[�ɑ��ĂłȂ��C���p���Ă��邱�̃z�[���y�[�W�̍�҂ɑ��čs�����̂Ƃ���D |
R1, R2�𖢒m���Ƃ���A���������𗧂Ă�D
�}�P���� R1+R2==5…(1)
�}�Q����==…(2)
(2)�̕������5R1R2=6(R1+R2)
5R1R2=6R1+6R2…(2’)
(1)���R1=5−R2��(2’)�ɑ�����������
5(5−R2)R2=6(5−R2)+6R2
25R2−5R22=30−6R2+6R2
5R22−25R2+30=0
R22−5R2+6=0
���̂Q���������������������ĉ���
(R2−2)(R2−3)=0
R2=2, 3
���̘A���������̉���
R2=2�̂Ƃ�R1=3
R2=3�̂Ƃ�R1=2
�����������������2
→�y���z(4)
|
||
|
�m���Q�n
�}�̒�R��H�ɂ����āC�[�qa, b�Ԃ̍�����RRab[��]�̒l��1.8R[��]�ł������B���̂Ƃ��C��R�̂������������̒�RRx[��]�̒l�Ƃ��āC�����͎̂��̂����ǂꂩ�B 
�@��ʍ��c�@�l�d�C�Z�p�Ҏ����Z���^�[���쐬�������
�@��O��d�C��C�Z�p�Ҏ����i�d���O��j����16�N�x�u���_�v��4 �@�Ȃ��C���y�щ���ɑ��鎿�ⓙ�́C�d�C�Z�p�Ҏ����Z���^�[�ɑ��ĂłȂ��C���p���Ă��邱�̃z�[���y�[�W�̍�҂ɑ��čs�����̂Ƃ���D |
R��Rx�̕���ڑ��ɂ�鍇����R��
����ɁCR��ڑ�����ƁCa, b�Ԃ̍�����R��
R+=1.8R
�ƂȂ邩��C���ӂ�R�Ŋ����
1+=1.8
�������
R+Rx+Rx=1.8R+1.8Rx
0.2Rx=0.8R
Rx=4R
→�y���z(4)
|
||
|
�m���R�n
�}�̂悤�ɁC��R�C�؊��X�C�b�`S�y�ѓd���v��ڑ�������H������B ���̉�H�ɒ����d��100[V]����������ԂŁC�}�̂悤�ɃX�C�b�`S���J�����Ƃ��d���v�̎w���l��2.0[A]�ł������B�܂��C�X�C�b�`S���@���ɕ����Ƃ��d���v�̎w���l�̓X�C�b�`2.5[A]�C�X�C�b�`S���A���ɕ����Ƃ��d���v�̎w���l��5.0[A]�ł������B���̂Ƃ��C��Rr[��]�̒l�Ƃ��āC�������͎̂��̂����ǂꂩ�B �������C�d���v�̓�����R�͖����ł�����̂Ƃ��C����덷�͂Ȃ����̂Ƃ���B 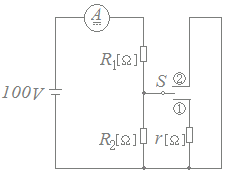
�@��ʍ��c�@�l�d�C�Z�p�Ҏ����Z���^�[���쐬�������
�@��O��d�C��C�Z�p�Ҏ����i�d���O��j����20�N�x�u���_�v��6 �@�Ȃ��C���y�щ���ɑ��鎿�ⓙ�́C�d�C�Z�p�Ҏ����Z���^�[�ɑ��ĂłȂ��C���p���Ă��邱�̃z�[���y�[�W�̍�҂ɑ��čs�����̂Ƃ���D |
���m����R1, R2, r�̂R����C�e�X�i�d���j=�i�d���j�~�i��R�j�ɂ����������R����̂ŁC�A���������ʼn�����B
�X�C�b�`S���J�����Ƃ� 100=2(R1+R2)…(1)
�X�C�b�`S���@���ɕ����Ƃ�
100=2.5(R1+)…(2)
�X�C�b�`S���A���ɕ����Ƃ�
100=5R1…(3)
�iR2�̗��[�ɂ͓d��������炸�CR2�ɂ͓d���͗���Ȃ��D����͇A���̓����̒�R��R�Ƃ����Ƃ��C�A��R2�Ƃ̍�����R
(3)���
��R→0�ƂȂ�Ɍ���0�ƂȂ邱�Ƃ���m���߂邱�Ƃ��ł���B
�j R1=20
�����(1)�ɑ�������
100=2(20+R2)
100=40+2R2
2R2=60
R2=30
������(2)�ɑ�������
100=2.5(20+)
40=20+
20=
�������
600+20r=30r
10r=600
r=60→�y���z(5)
|