|
回路に流れる電流,与えられた端子間の電圧,未知の抵抗の大きさなどを求めるときに次のキルヒホフの法則が用いられます.
【キルヒホフの第1法則】
≪解説≫
回路内のどの点についても,「入って来る電流」の大きさと「出ていく電流」の大きさは等しい。 【キルヒホフの第2法則】 どの閉回路についても「電圧降下」の合計と「起電力」の合計は等しい.
【キルヒホフの第1法則】
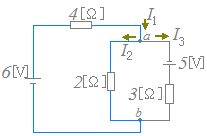
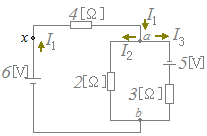
○ この法則は,電流については"湧き出し"も"吸い込み"もないことを表しており,回路の中のどんな点でも成り立ちますが,例えば図1の点xのような場所で「入って来る電流」I1と「出ていく電流」I1が等しいのは当然のことです.
○ キルヒホフの第1法則が役に立つのは,右図1の点aやbのような接続点(分岐のある点)です.
たとえば,点aにおいて入って来る電流をI1,出て行く電流をI2,I3とおくと,キルヒホフの第1法則により I1=I2+I3…(1)
が成り立ちます.

○ 電流I1,I2,I3の向きを右図1のように想定しましたが,実際に図ってみると例えば2[Ω]の抵抗に加わる電圧は上側よりも下側の方が高いかもしれません.すなわちI2は逆向きかもしれません.しかし,このような場合にはI2は計算結果として負の値になるようになっています.つまり,電流の向きは,初めの想定と同じ向きならば正の値,逆向きならば負の値になりますので,どちら向きに想定しても構いません.

○ 点aにおいて(1)の関係式が成り立つのならば,点bについても同様に方程式を立てることができるはずですが,
I2+I3=I1…(1’)
という式は,よく見ると(1)と同じものです.(点aから反時計回りに回ると,途中で分岐せずに点bにたどりつきます.このような場合,点aについて立てた方程式と点bについて立てた方程式は同じものになります.)この式の内容は正しいのですが,(1)を立ててさらに(1’)も書くと式がごちゃごちゃしてもつれてしまいます.連立方程式として解くときに式の個数が多過ぎると混乱してしまうことが多いので,(1)と(1’)はどちらか一方だけ書きます.  |
図1
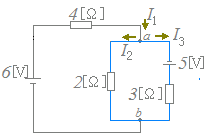
【キルヒホフの第2法則】
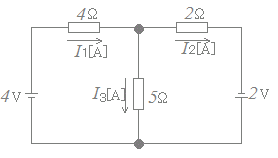
4I1+2I2=6…(2)
が成り立ちます.
3I3−2I2=5…(3)
が成り立ちます.
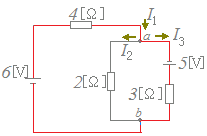
4I1+3I3=5+6…(4)
が成り立つように見えますが,もし(2)(3)を使うのなら(4)は使わないようにしましょう.(これら3個のうち2個あればよく3個とも書くのはよくありません.) 実際,(2)+(3)のより(4)が得られ,(4)は何も新しいことを述べていないばかりでなく,式が多過ぎると連立方程式を解くときにもつれてしまって解けなくなります. 実際,(2)+(3)のより(4)が得られ,(4)は何も新しいことを述べていないばかりでなく,式が多過ぎると連立方程式を解くときにもつれてしまって解けなくなります.この問題では,未知数はI1,I2,I3の3個で,方程式は(1)(2)(3)の3個でちょうど解けます.(4個あっても困るのです.) I2が2回登場しますが,これは問題なく,すべての閉回路について電圧降下が検討されるようにします. |
|
【未知数が3個ある連立方程式の解き方】 キルヒホフの法則を使って,上で検討したように連立方程式を立てると,次のような「未知数が3個」で「方程式が3個」の連立方程式になります.この連立方程式の解き方は高校で習いますが,ここで復習しておきます.
まず,1文字を消去して未知数が2個,方程式が2個の連立方程式にします. (1)を(2)(3)に代入してI1を消去して,I2, I3だけの方程式にします.
(2’)+(3’)×3により I2を消去して,I3 だけの一次方程式にします.
未知数が1個
方程式が1個 の一次方程式 I3について解けます. I3=21/13=1.62
解が1個求まる
(2’)か(3’)のどちらかに代入してI2を求めます.
|
図5 ・・・ 次の流れを頭の中に地図として覚えておくことが重要 【この地図を忘れると迷子になってしまう!】
階段を3→2→1と降りて行って,
1→2→3と登るイメージ 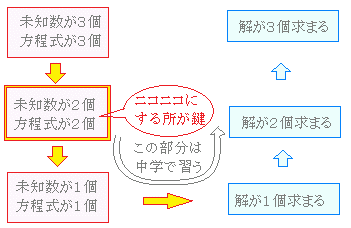 ※とにかく「2個2個」の連立方程式にするところが重要です.(そこら先は中学で習っているのでたぶん解けます.) よくある失敗は「一度に1個にしようとして間違ってしまう」「方程式の個数と未知数の項数が合わなくなってしまう」というような場合です.
左の結果を見るとI2=−0.08となっており,実際には2[Ω]の抵抗においては,電流は「下から上へ」流れていることになります.
このように「方程式を立てるときに想定する電流の向きは適当でよく,結果として逆向きになっているときは負の値になる」ことで分かります. |
||||||||||||
|
I1, I2, I3を未知数とする連立方程式を立てる.
上の接続点(分岐点)についてキルヒホフの第1法則を適用すると I1=I2+I3…(1)
左側の閉回路についてキルヒホフの第2法則を適用すると4I1+5I3=4…(2)
右側の閉回路についてキルヒホフの第2法則を適用すると2I2−5I3=2…(3)
(1)を(2)に代入してI1を消去すると4(I2+I3)+5I3=4
4I2+9I3=4…(2’)
(2’)−(3’)×2により I2を消去すると
19I3=0
I3=0
(3)に代入
I2=1
(1)に代入
I1=1
→【答】(3)
|
|||||||||||||
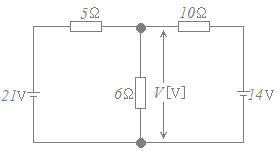
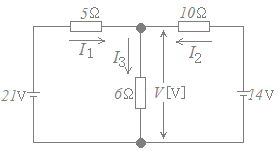 各抵抗に流れる電流を右図のようにI1, I2, I3とおく.
各抵抗に流れる電流を右図のようにI1, I2, I3とおく.上の接続点(分岐点)についてキルヒホフの第1法則を適用すると I1+I2=I3…(1)
左側の閉回路についてキルヒホフの第2法則を適用すると5I1+6I3=21…(2)
右側の閉回路についてキルヒホフの第2法則を適用すると10I2+6I3=14…(3)
(未知数にはもう1つVがあり,合計4個であるが,未知数4個の連立方程式としなくても,上記の結果が出てからV=6I3によって求めればよい…計算を簡単にする工夫)
(1)からI1=I3−I2…(1’)(1’)を(2)に代入してI1を消去する 5(I3−I2)+6I3=21
−5I2+11I3=21…(2’)
(3)より
5I2+3I3=7…(3’)
(2’)+(3’)によりI2を消去する14I3=28
I3=2(I1=, I2==)
ゆえに
V=6I3=12→【答】(4)
|
|||||||||||||
|
[問題3]
図のように,抵抗を直並列に接続した回路がある。この回路において,I1=100[mA]のとき,I4[mA]の値として,最も近いものを次の(1)〜(5)のうちから一つ選べ。 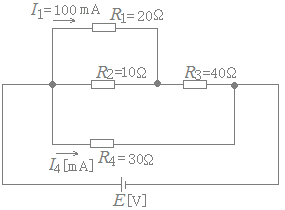
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成24年度「理論」問6 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. 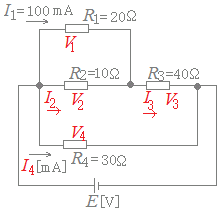 |
※1[mA]=0.001[A]を用いて,以下において,電流の単位を[A]で表す.
|
||||||||||||
|
[問題4]
図のように,既知の電流電源E[V],未知の抵抗R1[Ω],既知の抵抗R2[Ω]及びR3[Ω]からなる回路がある。抵抗R3[Ω]に流れる電流がI3[A]であるとき,抵抗R1[Ω]を求める式として,正しのは次のうちどれか。 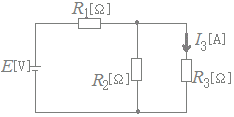 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成18年度「理論」問6 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. 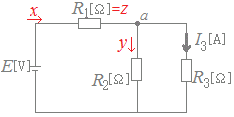 |
未知数を分かりやすくするために,左下図で示したように電流をx, y,抵抗R1をzで表す.
接続点aにおいてキルヒホフの第1法則を適用すると
x=y+I3…(1)
左側の閉回路についてキルヒホフの第2法則を適用すると
xz+yR2=E…(2)
右側の閉回路についてキルヒホフの第2法則を適用すると
yR2−I3R3=0…(3)
(3)より
y=
これを(1)に代入
x=+I3=I3
これらを(2)に代入
I3z+R2=E
I3z=E−I3R3
z=(E−I3R3)=(−R3)
=(−1)
→【答】(5)
|
||||||||||||
|
[問題5]
図のような直流回路において,電源電圧がE[V]であったとき,末端の抵抗の端子間電圧の大きさが1[V]であった。このとき電源電圧E[V]の値として,正しのは次のうちどれか。 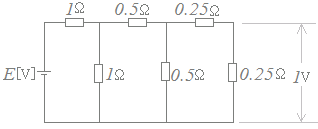
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成15年度「理論」問6 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. 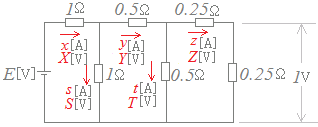 |
左下図のように未知の電流と電圧が5個ずつありますが,各々の抵抗が分かっているから,オームの法則V=IR(またはキルヒホフの第2法則)を用いると電流I・電圧Vのいずれか一方が分かれば,他方は求まります.
末端の抵抗0.25[Ω]に加わる電圧が1[V]だから,電流は
そこで,右側から順に電圧⇔電流を「将棋倒しのように」求めて行けます. 内容的には,x,y,z,s,t,Eの6個の未知数からなる6個の方程式の連立になりますが,これほど多いと混乱し易いので,「筋道を立てて算数的に」解く方が楽です. =4[A]
したがって
z=4[A]
Z=4×0.25=1[V]
右端の閉回路にキルヒホフの第2法則を適用
0.25×4+0.25×4−0.5t=0
t=4 (T=2)
キルヒホフの第1法則により
y=z+t=8 (Y=4)
真中の閉回路にキルヒホフの第2法則を適用
0.5y+0.5t−1s=0
s=4+2=6 (S=6)
キルヒホフの第1法則により
x=y+s=8+6=14 (X=14)
真中の閉回路にキルヒホフの第2法則を適用
1x+1s=E
E=14+6=20
→【答】(2)
|
||||||||||||
|
[問題6]
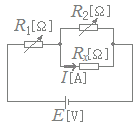
図のように,可変抵抗R1[Ω],R2[Ω],抵抗Rx[Ω],電源E[V]からなる直流回路がある。次に示す条件1のときのRx[Ω]に流れる電流I[A]の値と条件2のときの電流I[A]の値は等しくなった。このとき,Rx[Ω]の値として,正しいものを次の(1)〜(5)のうちから一つ選べ。 条件1:R1=90[Ω],R2=6[Ω]
条件2:R1=70[Ω],R2=4[Ω]
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成23年度「理論」問7 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. 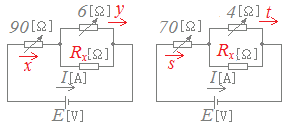 |
左下図のように未知数が電流x,y,s,t,I,抵抗Rx,電源Eの合計7個ありますが,IはEに比例するため,I,Eは定まりません.
キルヒホフの第1法則により
x,y,s,t,Rxの5個を未知数として方程式を5個立てれば解けます.(これらはIを使って表されます.) x=y+I…(1)
s=t+I…(2)
各々の小さな閉回路にキルヒホフの第2法則を適用
6y−IRx=0…(3)
4t−IRx=0…(4)
各々大回りの閉回路にキルヒホフの第2法則を適用
90x+6y=(E)=70s+4t…(5)
(1)(2)を(5)に代入してx,sを消去する
90(y+I)+6y=70(t+I)+4t
90y+90I+6y=70t+70I+4t
96y+20I=74t…(5’)
(3)(4)より
6y=4t…(6)
(6)を(5’)に代入
64t+20I=74t
20I=10t
t=2I
これを戻せば順次求まる
s=t+I=3I
y=t=I
x=y+I=I+I=I
Rx===8
→【答】(4)
|