|
金属の導体の中には,陽子と電子があり,陽子は自由に動けないが電子は自由に動くことができる.そこで,磁界の中で導線を動かすと,電子に電磁力が働いて移動する.これにより起電力を生じる.
■導線の両端に生じる起電力
この頁では,「フレミングの左手の法則」「フレミングの右手の法則」などと紛らわしいことを幾つも覚えずに,「フレミング左手の法則」だけを確実に使うという考え方で解説する.
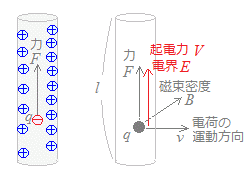
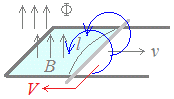
○ 右図1のように,磁束密度B[T]の磁界の中で,長さl[m]の導線を磁束に垂直な方向に速度v[m/s]で動かしたとき,導線の両端に生じる起電力V[V]は
(解説)
V=Bvl…(1)
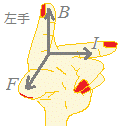
起電力の向きは,左手のFBIに当てはめたときの親指(F)の向きが正の電荷の行きたい方向(親指の元が正,親指の先が負)
※実際には,負の電荷を持った電子が動くのだから,親指の逆向きに電子が飛び,結果として親指の向きに電流が流れる.
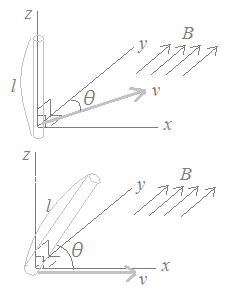
○ 右図2のように,導体の運動方向が磁束と垂直ではなく斜め(磁束となす角がθ[rad])であるとき,または導線と運動方向が垂直ではなく斜め(運動方向と導線のなす角がθ[rad])であるとき,
長さl[m]の導線が,1秒間にv[m]動くとき,vl[m2]の長方形を横切り,磁束密度がB[T]のとき,その長方形にBvlの磁束が含まれる.上の公式(1)は,起電力は1秒間に横切る磁束の本数に等しいことを示しているから,運動方向や導線などが斜めを向いているときは,1秒間に横切る磁束の本数を計算すればよいことになる.
運動方向や導線が直角ではなく,斜めの角θになっているとき
V=Bvlsinθ…(1’) 右図1の右側の図のように,電荷が磁界の中を運動すると,フレミング左手の法則により電荷は力を受ける.(実際には,電子の電荷は負なので逆向きになるが,これは後で向きを変えればよいとして,とりあえず大きさを求める.)
F=Bqv
ところで,電荷q[C]にかかる力F[N]と電界の強さE[V/m]には
F=qE
の関係があるから,電界の強さは
E=Bv
したがって
V=El=Bvl
|
図1
   |
|
■電磁誘導のファラデーの法則
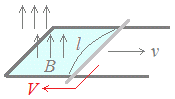
右図3は,コの字形の固定の導線枠組みに対して,磁界が下から上に向かっているときに,自由に動ける導線の一辺を右に向かって動かしたときに発生する起電力を示しています.
ここでは,あくまで「フレミングの左手の法則」で解説しています.
○ 起電力の大きさは,
V=Bvl
○ 起電力の向きは,図4の親指の向きです.
ところで,この起電力の「大きさ」と「向き」を,閉回路を貫く磁束の本数で説明する方法があり,これによりコイルに発生する起電力を一般的に説明できます.
電磁誘導による起電力を,電磁場における「保守性」を表すものと解釈し,磁束が増える方向に変化しているときはそれを減らす方向に,磁束が減る方向に変化しているときはそれを増やす方向に起電力が働くと考えるところがポイントです.
(1) [起電力の向き]
一辺が右に動くと,図3の(コの字形)+(一辺)からなる四角形を貫く磁束の本数は「増加」します. → これを打ち消す方向に,起電力が発生します.すなわち,図5の青色の矢印の向きに磁界が発生するように(アンペアの法則により)赤色で示した電流が流れます.
(2) [起電力の大きさ]
一辺が右に動くと,図3の(コの字形)+(一辺)からなる四角形を貫く磁束の本数は,1秒間あたりBvl本だけ「増加」します. → これを打ち消す方向に,起電力が発生します.すなわち,図5において長方形の枠を貫く磁束の本数をΦとおくとき,1秒間当たりのΦの変化は+Bvlですが,これを打ち消す大きさで起電力が発生します.
V=−=−Bvl
【電磁誘導のファラデーの法則[要約]】
○ 閉回路を貫く磁束の本数をΦとおくとき,
V=−
(Vの向きは,Φの増減を打ち消す向きで,その大きさはΦの変化率に等しい)
○ コイルの巻き数がN回であるときは
V=−N
|
図3
電磁誘導のファラデーの法則を使うと,次のような磁石とコイルの関係も説明できます.
次の図においては磁石が固定されていて,コイルが動くものとする. ○ 図6では,コイルが右に動くとコイルの中の磁束が減少するので,青の矢印の向きに磁場が生じるように赤の矢印の向きに電流が流れます. ○ 図7では,コイルが左に動くとコイルの中の磁束が増加するので,青の矢印の向きに磁場が生じるように赤の矢印の向きに電流が流れます. 図6 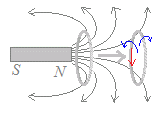 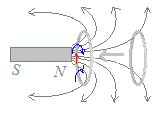 |
|
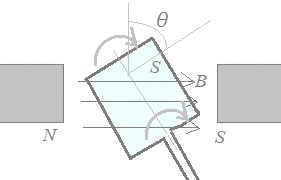
■発電機の原理
右図8のように一様な磁界の中でコイルを回転させるものとする.磁束密度をB[T],コイルの面積をS[m2],コイルの面が磁界に垂直な平面となす角をθ,コイルの回転の角速度をω[rad/s]とすると
θ=ωt
時刻tにおいてコイルの面を貫く磁束Φは
Φ=BScos(ωt)
したがって,ファラデーの電磁誘導の法則により,起電力は
V=−=BSω sin(ωt)
となって,最大値が磁束密度B,コイルの面積S,角速度ωに比例する正弦波交流の起電力を生ずる.
|
図8
 |
|
[問題1]
図1のように,磁束密度B=0.02[T]の一様な磁界の中に長さ0.5[m]の直線状導体が磁界の方向と直角に置かれている。図2のようにこの導体が磁界と直角を維持しつつ磁界に対して60°の角度で,矢印の方向に0.5[m/s]の速さで移動しているとき,導体に生じる誘導起電力e[mV]の値として,最も近いのは次のうちどれか。 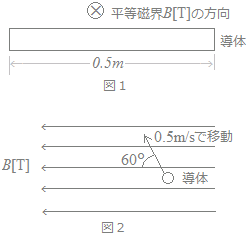 (1)2.5 (2)3.0 (3)4.3 (4)5.0 (5)8.6 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成16年度「理論」問3 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
e=BvlsinθにB=0.02,v=0.5,l=0.5,θ=60°を代入
e=0.02×0.5×0.5×sin60°=0.0043[V]
だから
e=4.3[mV]
→【答】(3)
|
|
[問題2]
紙面に平行な水平面内において,0.6[m]の間隔で張られた2本の直線状の平行導線に10[Ω]の抵抗が接続されている。この平行導線に垂直に,図に示すように,直線状の導体棒PQを渡し,紙面の裏側から表側に向かって磁束密度B=6×10−2[T]の一様な磁界をかける。ここで,導体棒PQを磁界と導体棒に共に垂直な矢印の方向に一体の速さv=4[m/s]で平行導線上を移動させているときに,10[Ω]の抵抗に流れる電流I[A]の値として,正しいのは次のうちどれか。 ただし,電流の向きは図に示す矢印の向きを正とする。また,導線及び導体棒PQの抵抗,並びに導線と導体棒との接触抵抗は無視できるものとする。 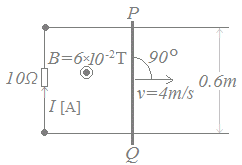 (4)0.0144 (5)0.0288 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成22年度「理論」問3 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
○V=Bvlで考える場合
V=6×10−2×4×0.6=14.4×10−2=0.144[V]

オームの法則により
0.144=10×I
I=0.0144[A]
起電力,したがって電流の向きは右図により正の向き
→【答】(3)
○ファラデーの法則で考える場合
磁束の増加率は
V=−=−6×10−2×4×0.6=−14.4×10−2=−0.144
だから,磁束が増える電流の向きQ→Pを正の向きとして
V=−0.144 オームの法則により −0.144=10×I I=−0.0144[A](Q→P向き) I=0.0144[A](P→Q向き) →【答】(3)
|