|
■フレミングの左手の法則
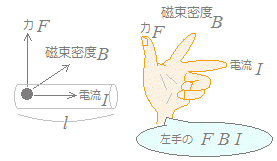
○ 磁界の中に電流を流すと,右図1のように電流と磁界の両方に垂直な方向に力が働きます.これを「フレミングの左手の法則」といいます.
左手の中指を電流の向きに,人差し指を磁界の向きに向けたとき,(電流が流れている導体が受ける)力は親指の向きになります.

F=BIl …(1)
※磁界の強さH[A/m]で書かれる法則も多くありますが,この法則は磁束密度B[T](テスラ:人名)Wb/m2を使って書かれていることに注意しましょう.
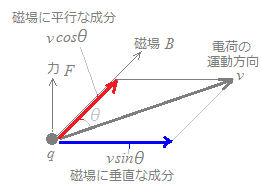
○ 右図2のように,電流が磁界に対して斜めに向いて流れているときは,電流のうちで磁界に平行な成分は力には関係なく,電流のうちで磁界に垂直な成分だけがこの力に関係します.
透磁率をμとするとき,B=μHの関係になっています.
F=BIlsinθ …(1’)
※電流が磁界と垂直になっているときは,sin90°=1となって,(1)になります.つまり,(1’)の方が一般的な公式ですが,(1’)の方はsinθが付いている分だけ複雑なので,垂直ならば(1),斜めならば(1’)で対応するぐらいの考えでよいでしょう.
|
図1
 この教材では「覚えることはなるべく少なくして,すぐ確実に出ることだけに絞る」という考え方を薦めます.そこで,「電磁力」も覚えず,後で登場する右手の法則も覚えないことにして,「左手のFBIだけ」は確実に言えることを目指します. 図2 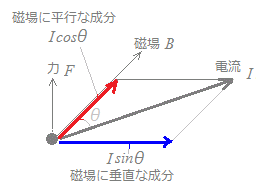 |
|
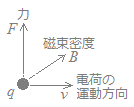
○ 磁界の中で荷電粒子(電荷)が運動をしているとき,図3のように電荷の向きと磁界の両方に垂直な方向に力が働きます. この力は「ローレンツ力」と呼ばれます.
電流は電荷の集まりなので,図1と図3とは同じ内容を表していることになります.
図3で電荷に働く力が集まって図1の導線を押していると考えるとよいでしょう.
○ 磁束密度をB[T],電荷をq[C],速度をv[m/s]とするとき,電荷に働く力F[N]は
F=Bqv …(2)
荷電粒子が電子のように負の電荷であるときは,力が逆向きになります.
○ 図4のように,荷電粒子の運動方向が磁界に対して斜めになっているときは,粒子の運動方向のうちの磁界に平行な成分は力に関係なく,磁界に垂直な成分だけがこの力に関係します.
F=Bqvsinθ …(2’)
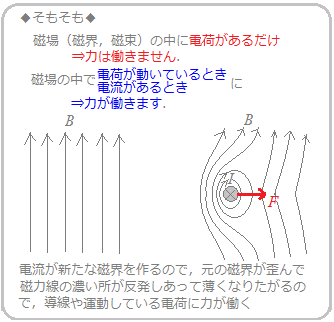 |
図3
※(1)と(2)は,1秒当たりの電荷(電気量)の動きに直してみると,同じ内容を表していることになります.
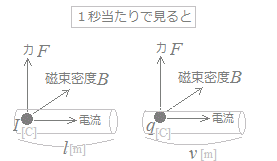
F=B×(Il)
(2)でq[C]の電荷が,v[m/s]の速さで飛んでいるとは,1秒間にq[C]の電荷がv[m]進むということです.
F=B×(qv)
違うのは,(1)では多くの電荷にかかる力をまとめてその入れ物となっている導体が受けると見なすのに対して,(2)では点電荷に力がかかると考える点です.
|
|
○ 磁場(磁束,磁界)の中で運動する荷電粒子に働く力,ローレンツ力については,次の点が重要です.
(1) 図4のように,磁界が紙面の表側から裏側に向いていて,荷電粒子が右図のように動いているとき,力は常に荷電粒子の運動方向と直角の向きに働きます.
この結果は,荷電粒子は円運動をします. 図4 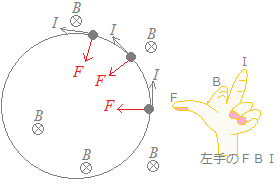
(2) 磁束密度をB[T],電荷をq[C],速度をv[m/s]とするとき,電荷に働く力F[N]は,上に述べたように
F=Bqv
になりますが,他方では力学において,等速円運動における向心力は,荷電粒子の質量をm[kg],速度をv[m/s],円の半径をr[m]とするとき,
F=m
となるので,
m=Bqv
r=
によって円運動の半径r[m]が求められます.
|
(参考) 等速円運動における速度,角速度,周波数,周期,加速度,向心力などの関係
円の半径をr[m],等速円運動の速度をv[m/s],角速度[角周波数]をω[rad/s]とすると
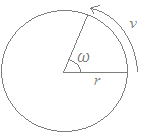
v=rω
ω=
●周波数をf[Hz]とすると,1回転が2π[rad]のところを1秒間にf回転するのだから
ω=2πf
f=
●周波数をf[Hz],周期をT[s]とすると,1秒間にf回転し,1回転するに要する時間がT[s]だから
T=
f=
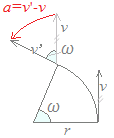 ●加速度a[m/s2]は,1秒間の速度vの変化v’−vだから
●加速度a[m/s2]は,1秒間の速度vの変化v’−vだから
a=vω
v=rωを代入すると
a=rω2
a=
●向心力をF[N]とすると,F=maだから
f=mvω
f=mrω2
f=m
※向心力が実在の力であるのに対して,遠心力はが円運動をしている物体に沿って座標系を動かしたときに現れる見かけの力です,等速円運動においては観測者が物体に乗っていると「向心力と遠心力が等しくなって釣り合う」と考えると半径が一定の円周上にあるように扱えて便利になるので,遠心力という用語もよく使われます.
等速円運動のとき (向心力)=(遠心力) [向きは逆]
|
|
■平行な直線電流間に働く力
右図5のように,平行な2つの導線に各々I1[A],I1[A]の電流が「同じ向きに」流れていて,導線間の距離がr[m]であるとき ○
電流I1が電流I2の場所に作る磁界の強さH[A/m]は,アンペアの法則によって求めることができ
H=[A/m]
ここで,磁束密度B[T]は,真空中の透磁率μ0を用いて
B=μ0H
によって求めることができるので,電流I2の長さl2=1[m]が受ける電磁力の大きさは F=μ0I2×1=…(1) その向きは,図6の左手の親指を見ると,I1の側を向いていることが分かる.
もし,電流I2について長さl2[m]の導線に働く力を求めるのであれば
F=×l2
○ 同様にして
電流I2が電流I1の場所に作る磁界の強さH[A/m]は,アンペアの法則によって求めることができ
H=[A/m]
ここで,磁束密度B[T]は,真空中の透磁率μ0を用いて
B=μ0H
によって求めることができるので,電流I1の長さl1=1[m]が受ける電磁力の大きさは F=μ0I1×1=…(2)
※ (1)(2)は等しいので,電流I1の1[m]が電流I2から受ける電磁力と電流I2の1[m]が電流I1から受ける電磁力の大きさは等しく,逆向きになっていることになる.
その向きは,図7の左手の親指を見ると,I1の側を向いていることが分かる.直接に接しているわけではないが,重力などと同様に,作用と反作用の関係になっている.
もし,電流I1について長さl1[m]の導線に働く力を求めるのであれば
F=×l1
|
図5
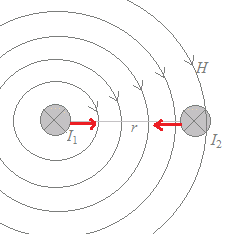 図6 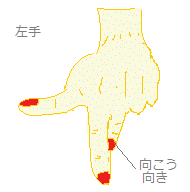  |
|
[問題1]
電流が流れている導体を磁界中に置くと,フレミングの(ア)の法則に従う電磁力を受ける。これは導体中を移動している電子が磁界から力を受け,結果として導体に力が働くと考えられる.
また,強さが一様な磁界中に,磁界の方向と直角に電子が突入した場合は,電子の運動方向と常に(イ)方向の力を受け,結果として等速(ウ)運動をすることになる.このような力を(エ)という. 上記の記述中の(ア),(イ),(ウ)及び(エ)に当てはまる語句として,正しいものを組み合わせたのは次のうちどれか. (ア)(イ)(ウ)(エ)
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成16年度「理論」11 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
フレミングの左手の法則だから,(ア)は[左手].
(イ)は[直角],(ウ)は[円],(エ)はローレンツ力 (1)←【答】 |
|
|
[問題2]
真空中において磁束密度B[T]の平等磁界中に,磁界の方向と直角に初速v[m/s]で入射した電子は,電磁力F=(ア)[N]によって円運動をする。
その円運動の半径をr[m]とすれば,遠心力と電磁力とが釣り合うので,円運動の半径はr=(イ)[m]となる。また円運動の角速度はω=[rad/s]であるから,円運動の周期はT=(ウ)[s]となる。 ただし,電子の質量をm[kg],電荷の大きさをe[C]とし,重力の大きさは無視できるものとする。 上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる式として,正しいものを組み合わせたのは次のうちどれか. (ア)(イ)(ウ)
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成19年度「理論」13 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
(ア)← ローレンツ力の公式によりF=Bev
(イ)←
m=Bev より r=
(ウ)←
ω=
f=
T=
より
T====
(2)←【答】 |
|
|
[問題3]
次の文章は,図に示す「磁界中における電子の運動」に関する記述である。
真空中において,磁束密度B[T]の一様な磁界が紙面と平行な平面の(ア)へ垂直に加わっている。ここで,平面上の点aに電荷−e[C],質量m0[kg]の電子をおき,図に示す向きに速さv[m/s]の初速度を与えると,電子は初速度の向き及び磁界の向きのいずれに対しても垂直で図に示す向きの電磁力FA[N]を受ける。この力のために電子は加速度を受けるが速度の大きさは変わらないので,その方向のみが変化する。したがって,電子はこの平面上で時計回りに速さv[m/s]の円運動をする。この円の半径をr[m]とすると,電子の運動は,磁界が電子に作用する電磁力の大きさFA=Bev[N]と遠心力FB=v2[N]とが釣り合った円運動であるので,その半径はr=(イ)[m]と計算される。したがって,この円運動の周期はT=(ウ)[s],角周波数はω=(エ)[rad/s]となる。 ただし,電子の速さv[m/s]は,光速より十分小さいものとする。また,重力の影響は無視できるものとする。 上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる組合せとして,正しいものを次の(1)〜(5)のうちから一つ選べ。 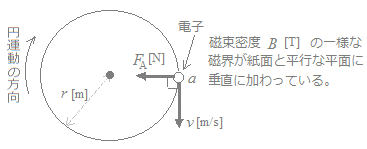 (ア)(イ)(ウ)(エ)
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成24年度「理論」12 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
 (ア)← 電子の電荷は負なので,電流の向きを電子の運動方向と逆向きにすると,右図のように力と電流の向きが当てはまる.このとき,磁界の向きは紙面の「おもてから裏」に向かう.
(ア)← 電子の電荷は負なので,電流の向きを電子の運動方向と逆向きにすると,右図のように力と電流の向きが当てはまる.このとき,磁界の向きは紙面の「おもてから裏」に向かう.(イ)← Bev=v2 より r== (ウ)← (設問の流れから自然に考えると)1周が2πrの円を速さvで回っているのだから,周期は T=== (次のように既存の公式から順に組み立てていっても求まる)
T=
f=
ω=
より
T====
(エ)←
ω===
(2)←【答】 |
|
|
[問題4]
図1のように,真空中において強さが一定で一様な磁界中に,速さv[m/s]の電子が磁界の向きに対してθ[°]の角度(0[°]<θ[°]<90[°])で突入した。この場合,電子は進行方向にも磁界の向きにも(ア)方向の電磁力を常に受けて,その軌跡は,(イ)を描く。
次に,電界中に電子を置くと,電子は電界の向きと(ウ)方向の静電力を受ける。また,図2のように,強さが一定で一様な電界中に,速さv[m/s]の電子が電界の向きに対してθ[°]の角度(0[°]<θ[°]<90[°])で突入したとき,その軌跡は(エ)を描く。 上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはまる語句として,正しいものを組み合わせたのは次のうちどれか。 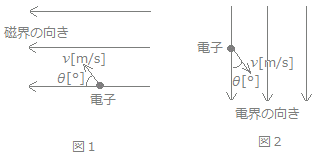 (ア)(イ)(ウ)(エ)
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成21年度「理論」12 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
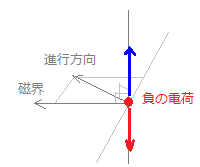 (ア) ← 右図のように進行方向と磁界の両方に対して,空間的に垂直な向きに電磁力が働き,その大きさは速さv[m/s]のうちで磁界に垂直な成分だけで決まります.ただし,電子の電荷は負なので逆向きになり,実際には右図の赤矢印の向きになります.
(ア) ← 右図のように進行方向と磁界の両方に対して,空間的に垂直な向きに電磁力が働き,その大きさは速さv[m/s]のうちで磁界に垂直な成分だけで決まります.ただし,電子の電荷は負なので逆向きになり,実際には右図の赤矢印の向きになります.[ア=直角] 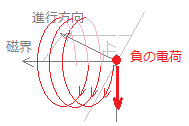 (イ) ← v[m/s]のうちで磁界に平行な向きの成分は変化せず等速で進み,磁界に垂直な向きの成分によって円運動を行うので,空間的にはこれらを組み合わせた「らせん」を描くことになります.
(イ) ← v[m/s]のうちで磁界に平行な向きの成分は変化せず等速で進み,磁界に垂直な向きの成分によって円運動を行うので,空間的にはこれらを組み合わせた「らせん」を描くことになります.[イ=らせん]  (ウ) ← 電界中で電荷が受ける力は電界の強さE[V/m]と電荷q[C]のみに関係し,電荷の速度には負関係です.(F=qE)
(ウ) ← 電界中で電荷が受ける力は電界の強さE[V/m]と電荷q[C]のみに関係し,電荷の速度には負関係です.(F=qE)正の電荷があると電界の向きに力(右図の青矢印)を受けますが,電子のような負の電荷があると,逆向き(右図の赤矢印)になります. [ウ=反対] (エ) ← 電子の電荷を−e[C],質量をm[kg]とし,初めの場所を原点として電界の向きをy座標に,図中の右向きをx座標にとったとき, ○ x方向については
Fx=0
だから,x方向の加速度はなく,等速運動となります.
x=(vsinθ)t…(1)
Fy=−eE
だから,y方向の加速度は
ay=−
y方向の速度は
vy=(vcosθ)−t
y座標は
y=(vcosθ)t−t2…(2)
となって,(1)(2)から時間tを消去するとyはxの2次関数になるので,放物線になります.
y=x−(x)2
[エ=放物線]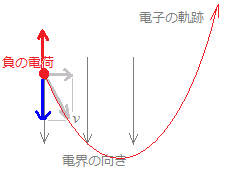 (5)←【答】 |
|
|
[問題5]
次の文章は,磁界中に置かれた導体に働く電磁力に関する記述である。
電流が流れている長さL[m]の直線導体を磁束密度が一様な磁界中に置くと,フレミングの(ア)の法則に従い,導体には電流の向きにも磁界の向きにも直角な電磁力が働く。直線導体の方向を変化させて,電流の方向が磁界の方向と同じになれば,導体に働く力の大きさは(イ)となり,直角になれば,(ウ)となる.力の大きさは,電流の(エ)に比例する。 上記の記述中の空白箇所(ア),(イ),(ウ)及び(エ)に当てはま組合せとして,正しいものを次の(1)〜(5)のうちから一つ選べ。 (ア)(イ)(ウ)(エ)
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成23年度「理論」3 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
 (ア) ← 右図のように電磁力が働き,フレミングの[左手]の法則と呼ばれる.
(ア) ← 右図のように電磁力が働き,フレミングの[左手]の法則と呼ばれる.(イ) ← F=BIlsinθにおいて, (平行な場合)θ=0 → sinθ=0 → F=0となるから[零] (ウ) ← F=BIlsinθにおいて, (直角の場合)θ=90° → sinθ=1となるから[最大] (エ) ← F=BIlsinθだから電流I(の1乗)に比例する. (5)←【答】 |
|
|
[問題6]
図に示すように,直線導体A及びBがy方向に平行に配置され,両導体に同じ大きさの電流Iが共に+y方向に流れているとする。このとき,各導体に加わる力の方向について,正しいものを組み合わせたのは次のうちどれか。 なお,xyz座標の定義は,破線の枠内の図で示したとおりとする。 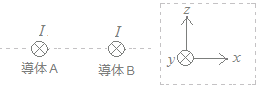 導体A導体B
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成22年度「理論」4 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
 導体Bに加わる力は,右図のように−x方向
導体Bに加わる力は,右図のように−x方向
 導体Aに加わる力は,右図のように+x方向
導体Aに加わる力は,右図のように+x方向
(2)←【答】 |
|
|
[問題7]
真空中に,2本の無限長直線状導体が20[cm]の間隔で平行に置かれている。一方の導体に10[A]の直流電流を流しているとき,その導体には1[m]当たり1×10−6[N]の力が働いた。他方の導体に流れている直流電流I[A]の大きさとして,最も近いものを次の(1)〜(5)のうちから一つ選べ。 ただし,真空中の透磁率はμ0=4π×10−7[H/m]である。 (1)0.1 (2)1 (3)2 (4)5 (5)10 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成24年度「理論」4 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
10[A]の電流が流れている導体に,他方のI[A]の無限長直線状導体が作る磁界の強さは
H=[A/m]
磁束密度B[T]は
B=μ0H=μ0=4π×10−7×[T]
10[A]の電流の長さ1[m]当たりが受ける電磁力の大きさは
F=4π×10−7××10×1
これが1×10−6[N]に等しいのだから
4π×10−7××10=1×10−6
I=0.1
(1)←【答】 |