|
【クーロンの法則】
(解説)
真空中にある2つの点電荷に働く力の大きさは,各々の点電荷の電気量の積に比例し,距離の2乗に反比例する. 真空中において,距離r[m]離れた位置にある電気量Q1, Q2[C]の電荷に働く力は F=[N]
クーロンの実験によれば,真空中の点電荷に働く力F[N]は「電気量の積に比例」し,「距離の2乗に反比例」する.そこで
F=k
と表せる. その比例定数kは,真空の誘電率ε0で表すことができ k= となる. ここで, ε0=8.854×10−12, =9×109 であるが,この数字を暗記する必要はない.
1[C]というのはとても大きな電気量で,1[C]の電荷2個を1[m]離して置くと(Q1=1, Q2=1, r=1のとき)F=9×109=9,000,000,000[N]の力が働くことになります.
右図1のように,力は2つの電荷を結ぶ方向に働き,同符号の電荷ときは反発力,異符号の電荷のときは引力になる. |
[用語と単位] 電荷
一つの物体がもっている電気量を電荷という.また,電荷という用語によって,電気を帯びた物体を表すこともある.
半径が無視できるほど小さい電荷のことを点電荷という. 電気量の単位:クーロン
電気量の単位はクーロンで,記号Cで表す.
※MKSA単位系,国際単位系では,
1[A](アンペア)の電流が1秒間流れたときに運ばれる電気量を1[C](クーロン)と定義する.
距離の単位としてメートル[m],重さの単位としてキログラム[kg],時間の単位として秒[s],電流の単位としてアンペア[A]を基本単位とし,他の単位はこれらから組み立てる. 力の単位:ニュートン
力の単位はニュートンで,記号Nで表す.
1[kg]の物体に1[m/s2]の加速度を生じさせる力を1[N]と定義する.
※誘電率εの媒質の中におけるクーロンの法則は F= になる. 図1 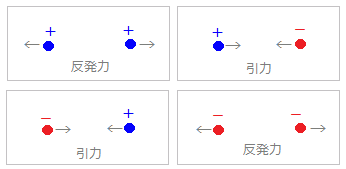 |
|
[問題1]
図のように,真空中の3[m]離れた2点A, Bにそれぞれ3×10−7[C]の正の点電荷がある。A点とB点とを結ぶ直線上のA点から1[m]離れたP点にQ[C]の正の点電荷を置いたとき,その点電荷にB点の方向に9×10−3[N]の力が働いた。この点電荷Q[C]の値として,最も近いのは次のうちどれか。 ただし,真空中の誘電率をε0=[F/m]とする。 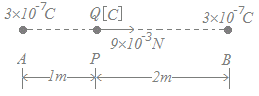
(4) 4.4×10−6 (5) 7.3×10−5
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成14年度「理論」問2 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
点電荷Q[C]に対してAの点電荷から右向けに働く力は
=9×109×3×10−7Q=27×102Q
点電荷Q[C]に対してBの点電荷から左向けに働く力は =9×109×=27×102× 右向きを正の向きとすると,これらの合力として右向きの力は 27×102Q−27×102×=27×102×=9×10−3 となるから Q=9×10−3×=×10−5=0.44×10−5 0.44に10を掛けて10−5を10で割ると 4.4×10−6 →【答】(4)
|
|
【ベクトルの和】
(解説)力は,図2のように「大きさ」と「向き」をもった量:ベクトルとして表されるので,1つの物体に2つ以上の力が働いているときに,それらの合力は単純に大きさを足したものにはならない. 2つの力の合力を「図形的に」求めるには (A) 右図3のように「ベクトルの始点を重ねて」平行四辺形を描き,その対角線が合力を表すと考える方法
(B) 右図4のように「1つ目のベクトルの終点に2つ目のベクトルの始点を接ぎ木して」考える方法
の2つの考え方がある.(どちらで考えてもよいが,どちらかしっかりと覚えることが重要.混ぜてはいけない.)
(A)の考え方では,右図3のように2人の人が荷物を引っ張っていると考える.このとき,荷物は力の大きさに応じて,結果的に「平行四辺形の対角線」の大きさと向きをもったベクトルになる.
(この考え方は,ベクトルを初めて習う人には最も分かりやすい.ただし,3つ以上のベクトルの和を求めるには,次に述べる三角形の方法の方が簡単になる.)
(B)の考え方では,右図4のようにベクトルを「物の移動」のモデルを使って考え,2つのベクトルととの和
=+ を,はじめにベクトルで表される「大きさ」と「向き」だけ移動させ,次にベクトルで表される「大きさ」と「向き」だけ移動させるものと考える.この場合,ベクトルの始点を,ベクトルの終点に重ねることがポイント. (A)で考えても(B)で考えても結果は同じであるが,3個以上のベクトルの和を求めるときは(B)の方が簡単になる.(右図4のように「しりとり」をして,最初の点から最後の点を結べば答えになる.)
【例1】
(考え方)右図6のように大きさ1[N]の2つの力が正三角形の2辺に沿って働いているとき,これらの力の合力を求めよ. 合力は右図の赤で示したになる. その大きさを求めるには,30°, 60°, 90°からなる直角三角形の辺の長さの比が1:2:になるということを覚えておく必要がある.(三平方の定理で求められるが,手際よく答案を作成するには,この三角形は覚えておく方がよい.) ただし,よくある間違いとして斜辺の長さはではなく2であることに注意:=1.732...<2 AE:AB:BE=1:2:だからABの長さ(大きさ)が1のとき, BE= このとき BD=2BE= したがって,右図BDの向きの大きさのベクトルになる.
【例2】
(考え方)右図7のように質量m[kg]の物体が糸で天井からつり下げられているとき,この物体に右向きにF[N]の力が働くと,この物体に働く力は,大きさmg[N](gは重力加速度[m/s2])の下向きの重力とFの合力となる. (1) 糸が鉛直下向きからなす角をθとするとき,tanθの値をm, g, Fで表せ. (2) 合力の大きさをm, g, Fで表せ. (1) 糸は合力の向きを向く. tanθ= (2) 合力の大きさは,三平方の定理を使って求めることができる |
 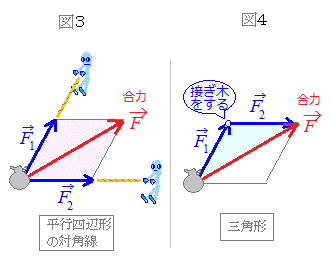 図5 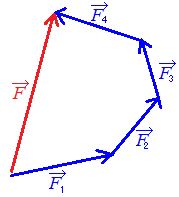 図6 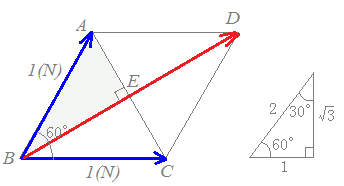 図7 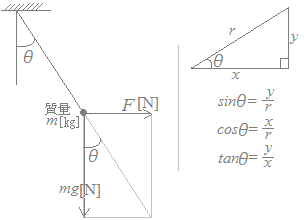 |
|
[問題2]
真空中において,図に示すように一辺の長さが30[cm]の正三角形の各頂点に2×10−8[C]の正の点電荷がある。この場合,各点電荷に働く力の大きさF[N]の値として,最も近いのは次のうちどれか。 ただし,真空の誘電率をε0=[F/m]とする。 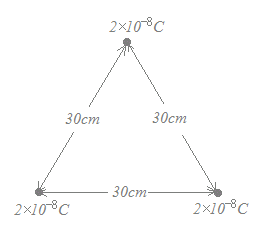
(4) 2.08×10−5 (5) 1.20×10−5
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成17年度「理論」A問題 問1 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
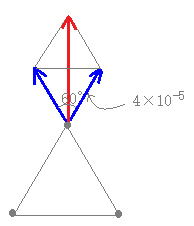 正三角形の上の頂点にある点電荷が他の点電荷から受ける1つの力(青線で示したもの)の大きさは
正三角形の上の頂点にある点電荷が他の点電荷から受ける1つの力(青線で示したもの)の大きさは
=9×109× = =100×4×10−7=4×10−5[N] 赤で示した合力の大きさは,その倍だから(上記の例1参照) 4×10−5×1.73=6.92×10−5[N] ※他の2つの点電荷に働く力も,向きだけが変わるが大きさはこれと同じ →【答】(1)
|
|
[問題3]
真空中において,それぞれ質量m[kg],電荷+Q[C]の小さな球の帯電体A及びBがある。これらの帯電体をそれぞれ長さr[m]の糸で点Pからつるしたところ,図のように,帯電体A,Bの間隔がa[m]となって静止した。 次の(a)及び(b)に答えよ。 ただし,真空の誘電率はε0[F/m],重力差速度はg[m/s2]とする。また,帯電体A及びBの直径はr[m]に比べて十分小さく,糸の質量は無視できるものとする。 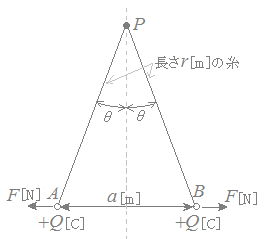
(1) (2) (3) (4) (5) HELP (b) 帯電体A,Bの静止状態において,糸の鉛直線に対する傾きがθ[°]であったときに成立する式として,正しいのは次のうちどれか。 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成15年度「理論」B問題 問15 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
(a)
AB間の距離はa[m]で,電荷は各々Q[C]だから F=[N] →【答】(5)
(b)
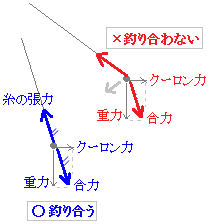 糸の向きが合力の向きと一致するときに静止し,向きが違えば静止しない.
糸の向きが合力の向きと一致するときに静止し,向きが違えば静止しない.下の図から tanθ== →Q2=4πε0a2mgtanθ…(1) また,斜辺の長さがr,底辺の長さがの直角三角形の図より sinθ== a=2rsinθ…(2) (2)を(1)に代入すると Q2=4πε0×4r2sin2θ×mgtanθ =16πε0r2mgr2sin2θtanθ 
→【答】(1)
|
|
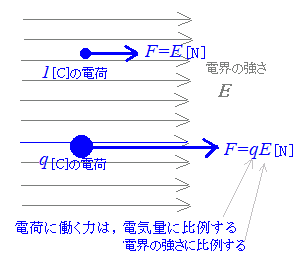
【電界の強さ】
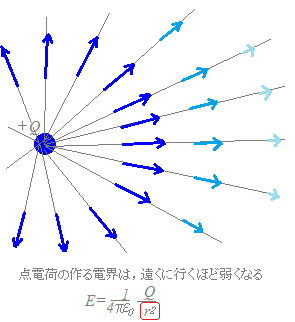
単位電荷1[C]に働くクーロン力(静電気力)の大きさを電界の強さといい通常E[V/m]で表す. 真空中において,電気量Q[C]の電荷から距離r[m]離れた位置に1[C]の電荷があるとき [N] の力が働き,q[C]の電荷があるとき [N] の力が働くから, 真空中において,電気量Q[C]の電荷から距離r[m]離れた位置の電界の強さは E=[V/m] 電界の強さがEのとき,q[C]の電荷に働く力は F=qE[N] |
図8
  |
|
[問題4]
真空中において,図のように一辺が2a[m]の正三角形の各頂点A,B,Cに正の点電荷Q[C]が配置されている。点Aから辺BCの中点Dに下ろした垂線上の点Gを正三角形の重心とする。点Dからx[m]離れた点Pの電界[V/m]の大きさを表す式として,正しいのは次のうちどれか。 ただし,点Pは点Dと点G間の垂線上にあるものとし,真空の誘電率をε0[F/m]とする. 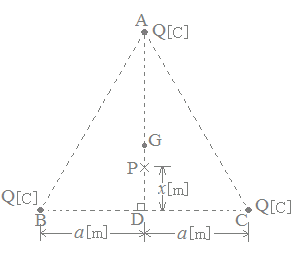
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成20年度「理論」A問題 問1 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
△ABCは正三角形だから,
AB=AC=2a(=BC) △ABDについて三平方の定理により AD==a 以上から AP=a−x また△BDP,△CDPについて三平方の定理により BP= 点Pに働く電界のうちB, Cに置かれた電荷による影響は,左右方向が相殺されるが,上下方向は等しく,各々 = 下向きを正の向きとすると, Aにおかれた電荷による電界の強さは B, Cにおかれた電荷による電界の強さは よって − →【答】(5)
|
|
[問題5]
図のように,真空中に電極間隔d[m]の平行板電極があり,陰極板上に電子を置いた。陽極板に電圧V[V]を加えたとき,この電子に加わる力F[N]の式として,正しいのは次のうちどれか。 ただし,電子の質量をm[kg],電荷の絶対値をe[C]とする。また,電極板の端効果は無視できるものとする。 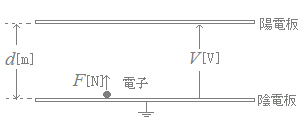
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成15年度「理論」問11 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
平行板電極の間では,電界の強さは一定で
E= したがって F=eE=e →【答】(5)
|
|
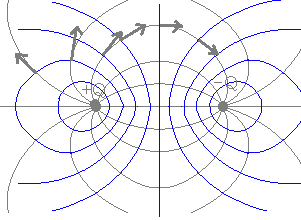
【電気力線と等電位面】
右図10は+Q[C]の電荷と−Q[C]の電荷によって作られる電気力線と等電位面を模式的に示したもので,黒色の線が電気力線,青色の線が等電位面を表す. (1) 黒色で示した電気力線は正の電荷から出て,負の電荷に入る. (2) 黒色で示した電気力線においては,各々の点の接線方向がその点での電界の向きを表している. (3) 黒色で示した電気力線は互いに交わらない. (4) 青色で示した等電位面は電気力線に垂直(直角)に交わる. (5) 青色で示した等電位面は,山の等高線とよく似た性質を持っており,等電位面が密になっている点では電界は強い. (6) 青色で示した等電位面も互いに交わらない. 右図11は平行板コンデンサの内部における電気力線と等電位面を模式的に示したもので,黒色の線が電気力線,青色の線が等電位面を表す. この場合にも,上記(1)〜(6)が成り立つ.特に,平行板コンデンサにおいては,電界の強さが一定で極板に垂直な直線になり,等電位面は等間隔で極板に平行な平面になる. |
図10
 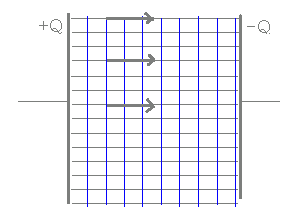 |
|
[問題6]
静電界に関する記述として,正しいのは次のうちどれか。 (1)二つの小さな帯電体の間に働く力の大きさは,それぞれの帯電体の電気量の和に比例し,その距離の2乗に反比例する。 (2)点電荷が作る電界は点電荷の電気量に比例し,距離に反比例する。 (3)電気力線上の任意の点での接線の方向は,その点の電界の方向に一致する。 (4)等電位面上の正電荷には,その面に沿った方向に正のクーロン力が働く。 (5)コンデンサの電極板間にすき間なく誘電体を入れると,静電容量と電極板間の電界は,誘電体の誘電率に比例して増大する. HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成21年度「理論」問2 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
(1)
F= だから,電気量の「積」に比例する.→ × (2) E= だから,「距離の2乗」に反比例する.→ × (3) (「向き」が前後2つの向きまで細かく指定するのに対して,「方向」とはこれらを区別せずに平行なものは同じ方向として扱うもの.) 電気力線の接線の「向き」は,その点の電界の「向き」に一致するから,当然「方向」も一致する. → ○ (4) 等電位面に垂直な方向に電気力線があり,クーロン力は等電位面に垂直に働く. → × (5) C=ε E= だから,静電容量は誘電率に比例するが,電界の強さは誘電率に反比例する. → × →【答】(3)
|