|
【はじめに】
○ 行列は,その要素の個数だけの独立した要素から成りたっており,次のように [ ] や( )で囲んで表します.
【行列式の求め方】 ○ 行列式の値を次のように定める理由については省略して,ここでは結論だけをまとめておきます.
※2次の行列式の値だけは,高校でも習うので覚えておくのが普通です
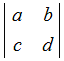 =ad−bc =ad−bc
0が多く含まれる1列目に沿って展開する
0− 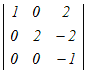 +0−0 +0−0さらに,0が多く含まれる1列目に沿って展開する =− 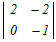 =−(−2−0)=2 → 3 =−(−2−0)=2 → 3
|
○この頁に登場する【問題】は,公益社団法人日本技術士会のホームページに掲載されている「技術士第一次試験過去問題 共通科目A 数学」の引用です.(=公表された著作物の引用)
○【解説】は個人の試案ですが,Web教材化にあたって「問題の転記ミス」「考え方の間違い」「プログラムの作動ミス」などが含まれる場合があり得ます. 問題や解説についての質問等は,原著作者を煩わせることなく,当Web教材の作成者(<浅尾>)に対して行ってください.
【例】 次の行列式の値を求めてください.
(1) 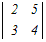
□ 例えば,1列目(縦)に沿って展開すると決める.
(2) □ 2には正の符号を,3には負の符号を付ける. 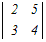 =2×4−3×5=8−15=−7 =2×4−3×5=8−15=−7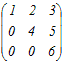
□ 0 が多く含まれる行や列に沿って展開すると計算が楽になります.ここでは,1列目に沿って展開します.
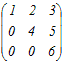 =1× =1×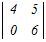 −0+0=24−0=24 −0+0=24−0=24(3) 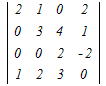
□ 0 が多く含まれる行や列に沿って展開すると計算が楽になります.ここでは,1列目に沿って展開します.
□ 4次の行列式←3次の行列式←2次の行列式のように次数を下げて計算します. 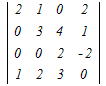 =2 =2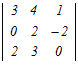 −0+0− −0+0−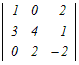 =2(3 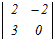 −0+2 −0+2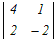 ) )−( 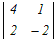 −3 −3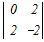 +0) +0)=2{3×6+2(−8−2)}−{(−8−2)−3×(−4)} =2{18−20}−{−10+2}=−4−2=−6 (4) 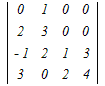
□ 0 が多く含まれる行や列に沿って展開すると計算が楽になります.ここでは,1行目に沿って展開します.
□ 4次の行列式←3次の行列式←2次の行列式のように次数を下げて計算します. 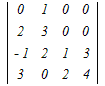 =0− =0−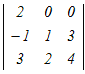 +0−0 +0−0さらに,1行目に沿って展開するのが有利 =−(2 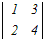 −0+0)=−2(4−6)=4 −0+0)=−2(4−6)=4
1列目に沿って展開する
x 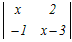 + +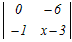 +0 +0=x(x(x−3)+2)+(0−6) =x(x2−3x+2)−6 =x3−3x2+2x−6=0 この3次方程式を因数分解によって解く x2(x−3)+2(x−3)=0 (x2+2)(x−3)=0 実数解は x=3 → 3 |
|
1列目に沿って展開する
t 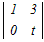 −0+(1−t) −0+(1−t)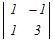 +0 +0=t(t−0)+(1−t)(3+1) =t2−4t+4=0 この2次方程式を因数分解によって解く (t−2)2=0 t=2 → 5 |
1列目に沿って展開する
0−4 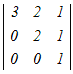 +0−0 +0−0さらに,1列目に沿って展開する =−4(3 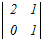 −0+0) −0+0)=−12(2−0) =−24 → 1 |
|
平成21年度技術士第一次試験問題[共通問題]
【数学】Ⅲ-18 3字行列式により定義される方程式 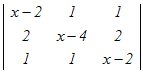 =0の解は,次のどれか. =0の解は,次のどれか.1−5, 0, 3 2−3, 0, 3 30, 3, 5 41, 3, 5 52, 3, 5 HELP
1列目に沿って展開する
(x−2) 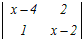 −2 −2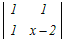 + +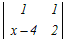 =0 =0=(x−2)(x2−6x+8−2)−2(x−2−1)+(2−(x−4)) =(x−2)(x2−6x+6)−2(x−3)+(−x+6)) =x3−8x2+18x−12−2x+6−x+6 =x3−8x2+15x=0 因数分解によって解く x(x2−8x+15)=0 x(x−3)(x−5)=0 x=0, 3, 5 → 3 |
平成22年度技術士第一次試験問題[共通問題]
【数学】Ⅲ-17 行列式により与えられる式 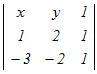 =0は,次のどの直線を表すか. =0は,次のどの直線を表すか.1x−y+1=02x+y+1=0 3x−y−1=0 4x+y−1=0 5x+y=0 HELP
1列目に沿って展開する
x 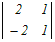 − −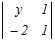 +3 +3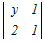 =0 =0x(2+2)−(y+2)−3(y−2)=0 4x−y−2−3y+6=0 4x−4y+4=0 x−y+1=0 → 1 |
|
1列目に沿って展開する
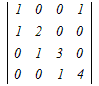 = =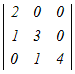 − −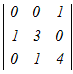 +0−0 +0−0各々の3次行例式を1行目に沿って展開する =2( 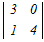 −0+0)−(0−0+ −0+0)−(0−0+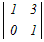 ) )=2(12−0)−(1−0) =24−1=23 → 4 |
1列目に沿って展開する
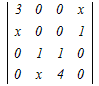 =3 =3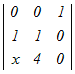 −x −x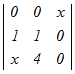 +0−0=0 +0−0=0各々の3次行例式を1行目に沿って展開する 3(0−0+ 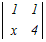 )−x(0−0+x )−x(0−0+x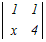 )=0 )=03(4−x)−x(x(4−x))=0 12−3x−4x2+x3=0 x3−4x2−3x+12=0 この3次方程式を因数分解によって解く x2(x−4)−3(x−4)=0 (x−4)(x2−3)=0 x=4, ± 自然数解は x=4 → 4 |
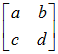
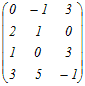
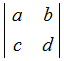
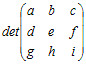
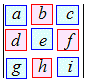
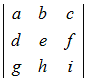 =a
=a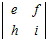 −d
−d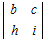 +g
+g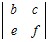
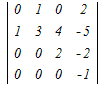 の値は,次のどれか.
の値は,次のどれか.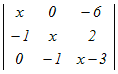 =0
=0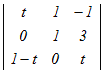 =0
=0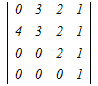 の値は,次のどれか.
の値は,次のどれか.