|
【コンデンサに蓄えられるエネルギー】
■(昔,高校で習った解説)静電容量C[F],電気量Q[C],電圧V[V]のコンデンサに蓄えられているエネルギーW[J]は
W=QV
Q=CVの公式を使って書き換えると
W=CV 2=
これらの公式は
C=ε
を使って表すこともできる.
この解説は,公式をきれいに導けて,結論は正しいのですが,筆者としては子供心にしっくりこないところがありました.詳しくは右下の※を見てください.
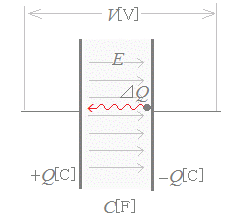
図1のようなコンデンサで,両極板の電荷が0の状態から電荷が各々+Q[C],−Q[C]に帯電させるまでに必要な仕事を計算する.そのために,図のように陰極板から少しずつ(ΔQ[C]ずつ)電界から受ける力に逆らって電荷を陽極板まで運ぶに要する仕事を求める.一般に+q[C]の電荷が電界の強さE[V/m]から受ける力は
F=qE[N]
コンデンサ内部における電界の強さは,極板間電圧V[V]とコンデンサの極板間隔d[m]で表すことができ
E=である.
したがって,ΔQ[C]の電荷が,そのときの電圧V[V]から受ける力は
F=ΔQ[N]
この力に抗してΔQ[C]の電荷を極板間隔d[m]だけ運ぶに要する仕事ΔW[J]は
ΔW=ΔQ×d=VΔQ=ΔQ[N]
この仕事を極板間電圧がV[V]になるまで足していけばよい.○ 初めは両極板は帯電していないので,E=0, F=0, Q=0
ΔW=ΔQ=0
○ 両極板の電荷が各々+Q[C],−Q[C]に帯電しているときの仕事は,上で検討したように
ΔW=ΔQ
→ これは,右図2の茶色の縦棒の面積に対応している.○ 最後の方になると,電荷が各々+Q0[C],−Q0[C]となり,対応する電圧,電界も強くなる. ○ 右図の茶色の縦棒の面積の総和W=ΣΔWが求める仕事であるが,それは図2の三角形の面積W=Q0V0になる. |
図1
 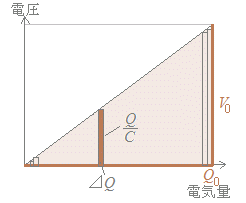 一般には,このような図形の面積は定積分
W=dQ=で求められる.
以上により,W=Q0V0=CV0 2=
※以上の解説について,筆者が「しっくりこない」「違和感がある」理由は2つあります. 1つ目は,両極板が帯電していない状態から電気を移動させて充電していくという解説方法で,「充電されたコンデンサにはどれだけの電気的エネルギーがあるか」という問いに答えずに「コンデンサを充電するにはどれだけの仕事が必要か」という「力学的エネルギー」の話にすり替わっています.(力学的エネルギーが電気的エネルギーに代わり,力学的+電気的エネルギーをひとまとめにしたエネルギーを考えると,エネルギー保存法則が成り立つのですが・・・) 2つ目は,コンデンサの内部は誘電体(=絶縁体)であるのに,そこに電気を通過させるに要する仕事を計算していることです.絶縁体には電気は通らないことになっていたはずだから,とても違和感がある. このような解説方法は「教える順序」に縛られて,まだ習っていない次の公式を使わないための「工夫」なのかもしれない.すなわち,次の公式を習っていれば上のような不自然な解説をしなくてもコンデンサに蓄えられるエネルギーの公式は導ける.
(エネルギー:仕事)=(ニュートン)×(メートル)
W=Fd
(エネルギー:仕事)=(クーロン)×(ボルト)W=QV
すなわち
Fd=W=QV …(1)
ただし(1)の公式はQやVが一定のときに成り立ち,コンデンサの静電エネルギーの公式を求めるときのようにQやVが0からQ0, V0まで増えていくときはが付くので,混乱しないように.
(1)の公式は
F=QE=Q(力は電界に比例する)
という既知の公式の両辺にdを掛けると得られる. その場合において,力Fが表すものは,図1においてはコンデンサの極板間にある電荷ΔQに与える外力,dは極板間隔であるが,下の図3においては力Fは金属の中を電荷が通るときに金属原子の振動などから受ける抵抗に抗して押していく力,dは抵抗の長さになる.(導体の中では抵抗はない) |
|
■(エネルギー)=(クーロン)×(ボルト)の関係を使った解説 右図3のようにコンデンサの極板に電荷がQ[C]だけ蓄えられている状態から始めて,通常の使用法の通りに抵抗を通して電気を流し,最終的に電荷が0になるまでに消費されるエネルギーを計算する.このとき,概念図も右図4のように変わる. なお,陽極板の電荷をQとおくとき,Q[C]の増分(増える分量)の符号を変えたもの−ΔQが流れた電荷となる. 変数として用いる陽極板の電荷QがQ0から0まで変化するときに消費されるエネルギーを計算することになる.(注意!) ○はじめは,両極板に各々+Q0[C],−Q0[C]の電荷が充電されているから, 電圧は
V=
消費されるエネルギーは(ボルト)×(クーロン)により
ΔW=(−ΔQ)=−ΔQ
しつこいようですが,Qは減少します.したがって,Qの増分ΔQ<0となり,−ΔQ>0であることに注意
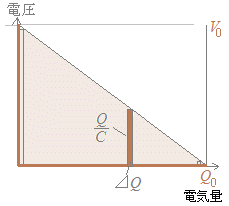
○ 両極板の電荷が各々+Q[C],−Q[C]に帯電しているときに消費されるエネルギーは
ΔW=−ΔQ
→ これは,右図2の茶色の縦棒の面積に対応している.○ 最後には,電気がなくなり,E=0, F=0, Q=0
ΔW=−ΔQ=0
○ 右図の茶色の縦棒の面積の総和W=ΣΔWが求めるエネルギーであるが,それは図4の三角形の面積W=Q0V0になる.この計算を,定積分で行うときは次の計算になる.
W=−dQ=
以上により,W=Q0V0=CV0 2= |
図3
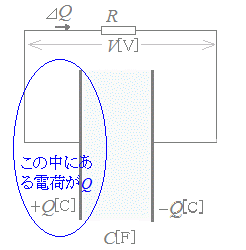  |
|
[問題1]
図に示す5種類の回路は,直流電圧E[V]の電源と静電容量C[F]のコンデンサの個数と組み合わせを異にしたものである。これらの回路のうちで,コンデンサに蓄えられる電界のエネルギーが最も小さい回路を示す図として,正しいのは次のうちどれか。 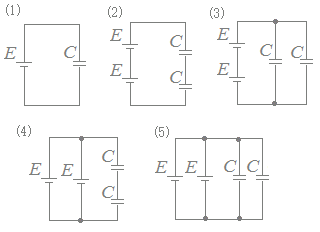
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成21年度「理論」問5 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
電圧をE[V],静電容量をC[F]とすると,コンデンサに蓄えられるエネルギーは
W=CE2
(1)
W=CE2
(2)電圧は2E コンデンサの直列接続による合成容量をC’とおくと
=+=
C’=
エネルギーは
W=(2E)2=CE2
(3)電圧は2E コンデンサの並列接続による合成容量はC’=C+C=2C エネルギーは
W=2C(2E)2=4CE2
(4)電圧はE コンデンサの直列接続による合成容量C’は
C’=
エネルギーは
W=E2=CE2
(5)電圧はE コンデンサの並列接続による合成容量はC’=C+C=2C エネルギーは
W=2CE2=CE2
(4)<(1)<(2)=(5)<(3)となるから
→【答】(4)
|
|
[問題2]
静電容量がC[F]と2C[F]の二つのコンデンサを図1,図2のように直列,並列に接続し,それぞれにV1[V],V2[V]の直流電圧を加えたところ,両図の回路に蓄えられている総静電エネルギーが等しくなった。この場合,図1のC[F]のコンデンサの端子間電圧をVc[V]としたとき,電圧比||の値として,正しいのは次のどれか。
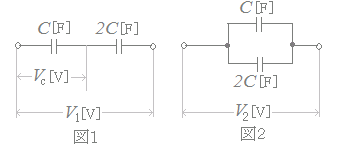
(1) (2) (3) (4) (5) 3.0 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成19年度「理論」問4 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
コンデンサの合成容量をC’[F]とおくと
図1では
=+=
C’=C
W=C’V12=CV12=CV12
図2では
C’=C+2C=3C
W=C’V12=3CV22
これらが等しいから
CV12=3CV22
V22=V12
V2=V1…(1)
また,図1においてコンデンサ2Cに加わる電圧をV2cとすると,Vc:V2c=2C:C=2:1(静電容量の逆の比)だから
Vc:V1=2:3
Vc=V1…(2)
(1)(2)より
Vc:V2=V1:V1=2:=:1
→【答】(4)
|
|
[問題3]
図の回路において,スイッチSが開いているとき,静電容量C1=0.004[F]のコンデンサには電荷Q1=0.3[C]が蓄積されており,静電容量C2=0.002[F]のコンデンサの電荷はQ2=0[C]である。この状態でスイッチSを閉じて,それから時間が十分に経過して過渡現象が終了した。この間に抵抗R[Ω]で消費された電気エネルギー[J]の値として,正しいのは次のうちどれか。 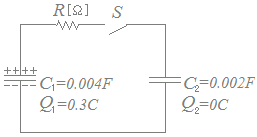 HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成14年度「理論」問9 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
(考え方1)
コンデンサに蓄えられるエネルギー
W=
を各々のコンデンサに対して適用し,エネルギーの総和を比較する.前
W=+=11.25[J]
後(←電圧が等しくなると過渡現象が終わる)
V1=V2 → = → Q1=2Q2…(1)
Q1+Q2=0.3…(2) (1)(2)よりQ1=0.2, Q2=0.1
W=+=7.5[J]
差は
11.25−7.5=3.75[J]
→【答】(2)
(考え方2)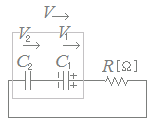 右図のようにコンデンサが直列接続されているものと見なし,各々のコンデンサにかかる電圧をV1, V2とする.ただし,上の解説とは異なりV1, V2の向きを右図のように決め,V=V1+V2が0になったら電流は流れなくなると考える.
右図のようにコンデンサが直列接続されているものと見なし,各々のコンデンサにかかる電圧をV1, V2とする.ただし,上の解説とは異なりV1, V2の向きを右図のように決め,V=V1+V2が0になったら電流は流れなくなると考える.直列コンデンサの合成容量は
=+=
C=
はじめの電圧は
V=V1+V2=+=
はじめのエネルギーは
W=CV 2=()2=3.75
後の電圧は
V=V1+V2=0
したがって,後のエネルギーは
W=CV 2=0
差は
3.75[J]
→【答】(2)
|
|
[問題4]
次の文章は,平行板コンデンサに蓄えられるエネルギーについて述べたものである。
極板間に誘電率ε[F/m]の誘電体をはさんだ平行板コンデンサがある。このコンデンサに電圧を加えたとき,蓄えられるエネルギーW[J]を誘電率ε[F/m],極板間の誘電体の体積V[m3],極板間の電界の強さE[V/m]で表現すると,W[J]は,誘電率ε[F/m]の(ア)に比例し,体積V[m3]に(イ)し,電界の大きさE[V/m]の(ウ)に比例する。 ただし,極板の端効果は無視する。 上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる語句として,正しいものを組み合わせたのは次のうちどれか。
(ア)(イ)(ウ)
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成20年度「理論」問2 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
コンデンサに蓄えられるエネルギーは
W=CV 2
で与えられ,平行板コンデンサの静電容量を誘電率ε,極板間の距離dで表すと
C=ε
また,電圧Vを極板間の距離dと電界の大きさEで表すと
V=Ed
したがって,
W=ε(Ed) 2=εSdE 2
ここで,極板間の誘電体の体積をv[m3]で表すと(記号が紛らわしくならないように電圧の記号Vと区別する)
v=Sd
W=εvE 2
ゆえに,誘電率εの「1乗」に比例し,体積vに「比例」し,電界の大きさEの「2乗」に比例する.
→【答】(4)
|
|
[問題5]
直流電圧1000[V]の電源で充電された静電容量8[μF]の平行平板コンデンサがある。コンデンサを電源から外した後に電荷を保持したままコンデンサの電極板間距離を最初の距離のに縮めたとき,静電容量[μF]と静電エネルギー[J]の値の組合せとして,正しいものを次の(1)〜(5)のうちから一つ選べ。
静電容量静電エネルギー
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成23年度「理論」問2 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
平行平板コンデンサの電極板間隔とエネルギーの関係
C=ε
により,電極板間隔dが小さくなるとCが大きくなる.
はじめは(Cはdに反比例する.) Qが一定のときCが大きくなると W= により,Wが小さくなる.(Wはdに比例する.) なお, V= により,Vも小さくなる.(Vもdに比例する.)
C=8[μF]
W=CV2=×8×10−6×10002=4[J]
電極板間隔を半分にすると,静電容量が2倍になり,静電エネルギーが半分になるから
C=16[μF]
W=2[J] →【答】(2)
|