|
■電気回路の計算に複素数を使うわけ
≪概要≫
量子力学のような分野においては,電子の状態を記述するために,複素数はなくてはならないものですが,電気回路において,電流や電圧の状態は微分方程式で記述することができるので,複素数がなければ調べられないということはありません. しかし,「周波数(したがって,角速度ω)が1種類だけしか登場しない交流」においては,複素数を使うと微分や積分の計算が掛け算・割り算に置き換えることができ,「計算が格段に簡単になる」事情があるので,交流は複素数で調べる方が便利になります. このように,交流を複素数で表すのは,単に便利だからで,交流と複素数とが切り離せないものだからではありません.ただ,複素数がよく分からないという方には,複素数を使うと重荷になりますので,この頁では複素数について必要最小限の内容を復習します.
≪少しだけ具体的な話でイメージ作り≫
○ 角速度(角周波数)をωとするとき,回路における電圧や電流は,Vmsin(ωt−θ), Imsin(ωt−α)のような実数値になります(Vm, Imは各々の最大値[振幅]). しかし,これらは
V=Vmei(ωt−θ)=Vm(cos(ωt−θ)+i sin(ωt−θ))
という複素数の虚部(虚数軸[縦軸]への投影)となっており,必要なときに複素数の虚部を取り出すことにしておいて途中経過は複素数で表すことができます.I=Imei(ωt−α)=Im(cos(ωt−α)+i sin(ωt−α)) ○ 指数関数の微積分については,係数が実数であっても複素数であっても,次の関係が成り立ちます.
eat+b=a eat+b
eat+bdt=eat+b+C
したがって
V=jωVmei(ωt−θ)=iωV
I dt=Imei(ωt−α)=I (C=0とする)
のように,微分はiωの掛け算に,積分はiωの割り算に置き換えることができます.
右に続く→
|
→続き
図1
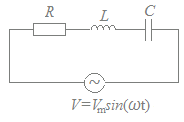
VR=RI
VL=L
VC==I dt
となるので,与えられた電圧V=Vmsin(ωt)に対する電流Iを求めるためには,キルヒホフの法則を使って
RI+L+I dt=Vmsin(ωt) …(*1)
もしくは,その両辺をtで微分した2階微分方程式
R+L+I=ωVmcos(ωt) …(*2)
を解くことになります.実数だけで電流を求めるためには,このように微分方程式を解く必要がありますが,これに対して上記のように複素数の性質を利用すると,(*1)は
RI+iωLI+I=Vmeiωt
(R+iωL+)I=Vmeiωt
となって,両辺をIの係数R+iωL+で割れば解が得られることになります.このように,複素数を使って表現すると,微分方程式を解く代わりに掛け算,割り算で解けるようになり,簡単に計算できるようになるので,1種類の角速度だけが登場する交流回路においては,電圧や電流を複素数で表します. |
|
■複素数とは,数学の複素数と電気回路の複素数の違い
高校数学IIにおいて,(x+4)2=−3のような,2乗して負の値になるような値を求める方程式を解くために,虚数を導入します.
x2=−1 → x=±=±i (x+4)2=−3 → x+4=±=±i x=−4±i このように,虚数単位i=と実数a, bを用いて, a+bi
の形で書かれる数を複素数と言います.(実部aと虚部bという複数の要素から成り立っているので複素数) ただし,
(1) 電気回路では電流を表すために文字iを使うので,混乱しないように虚数単位をjで表します.
(2) 数学では虚数単位iを後に書くことが多いですが,電気関係の本ではjを前に書きます.
|
【問題1】 次の複素数について虚部を答えてください.
複素数a+biのうちのiの係数bの部分を虚部といいます.
したがって,3−4i=3+(−4)iの虚部は,−4になります.
複素数a+biのうちのiの係数bの部分を虚部といいます.
したがって,cos(ωt)+i sin(ωt)の虚部は,sin(ωt)になります.
複素数a+biのうちのiの係数bの部分を虚部といいます.
したがって,cos(ωt+α)+i sin(ωt+α)の虚部は,sin(ωt+α)になります. |
|
■複素数と(2次元)ベクトルの関係
○「大きさ」と「向き」をもつ量を表すためにベクトルを使います.以下においては,2次元(平面上の)ベクトルだけを扱います.
図2 
=(3, 4), =(−4, 5)
のように(x成分,y成分)をカンマで区切って表し,初めに書いた数字がx成分,2番目に書いた数字がy成分を表すものと決めます.このとき,(3, 4)と(4, 3)は異なるベクトルになります.○ 複素数はz=3+4iのように表します.これはベクトル(3, 4)に対応しています. 図3 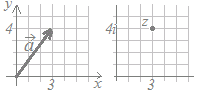 |
【問題2】 次の図の各ベクトルを成分で答えてください. 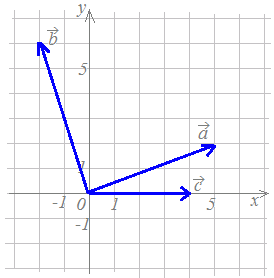
ベクトルを成分で表示するには,(x成分,y成分)のようにカンマで区切って表します.
したがって,=(5, 2)
初めに,原点から横方向への移動x成分を読み取り,次に原点から縦方向への移動y成分を読み取ります.
したがって,=(−2, 6)
初めに,原点から横方向への移動x成分を読み取り,次に原点から縦方向への移動y成分を読み取ります.
したがって,=(4, 0) |
|||||||||||||||||||||
|
【問題3】 次の図の各複素数を答えてください. 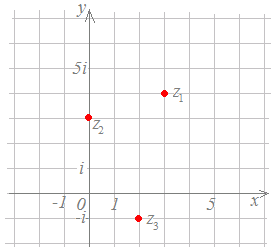
初めに,原点から横方向への移動で実部を読み取り,次に原点から縦方向への移動で虚部を読み取り,a+biの形で答えます.
したがって,z1=3+4i |
初めに,原点から横方向への移動で実部を読み取り,次に原点から縦方向への移動で虚部を読み取り,a+biの形で答えます.
したがって,z2=3i
初めに,原点から横方向への移動で実部を読み取り,次に原点から縦方向への移動で虚部を読み取り,a+biの形で答えます.
したがって,z3=2−i |
|||||||||||||||||||||
■ベクトル・複素数の和差,実数倍
ベクトル
(1) (2, 3)+(4, 5)=(6, 8)
複素数
(2) (2, 3)−(4, −5)=(−2,8)
(3) (cosωt, sinωt)+(cos(ωt+), sin(ωt+)
=(cosωt+cos(ωt+), sinωt+ sin(ωt+)
(4) 3(2, 3)−2(4, −5)=(6, 9)−(8, −10)=(−2, 1)
(1) (2+3i)+(4+5i)=6+8i
(2) (2+3i)−(4−5i)=−2+8i
(3) (cosωt+i sinωt)+i(cos(ωt+)+i sin(ωt+))
=(cosωt+cos(ωt+)+i(sinωt+ sin(ωt+))
(4) 3(2+3i)−2(4−5i)=6+9i−8+10i=−2+i |
【問題4】 次のベクトルの成分を求めてください.
x成分とy成分を分けて求めます.
x成分は2−4=−2 y成分は−3+5=2 (−2, 2)…(答)
x成分とy成分を分けて求めます.
x成分は2−5=−3 y成分を計算するときに,「かっこ」の外し方に注意します.3−(−6)=3+6=9 (−3, 9)…(答)
はじめに「かっこ」を外し,次に各成分を求めるとよいでしょう.
【問題5】(−4, 8)+(−3, 6)=(−7, 14)…(答) 次の複素数を求めてください.
実部と虚部を分けて計算します.
(3−1)+(−4+7)i=2+3i…(答)
はじめに「かっこ」を外し,次に実部と虚部を分けて計算します.
2(−3+4i )−3(1−2i )=−6+8i−3+6i =(−6−3)+(8+6)i=−9+14i…(答) |
|
■複素数の積商
ベクトルについては,いわゆる掛け算や割り算というものを考えません.(内積,外積というものはありますが,割り算は考えません.)
複素数の積商(掛け算,割り算)は,虚数単位iを他のa,b, c,...,x, y, z,...などの文字と同様に計算できます.ただし,その定義に従ってi2が登場したら−1にします.【例】
(1) (2+3i)(4+5i)=8+10i+12i+15i2=8+10i+12i−15
=−7+22i (2) (2+3i)2=4+12i+9i2=4+12i−9 =−5+12i
(3)
※分母に虚数a+biがあるときは,無理数の分母有理化と類似の変形により,分母と分子にその共役複素数a−biを掛けて,分母を実数に変えます.この変形により,全体を実部と虚部に分けることができるようになります.上記の式では,分母1+2iの共役複素数1−2iを分母と分子に掛けます.
===
=…(*)
=(−)+(−)i
慣れてきたら(*)の形で答えてよい.
|
【問題6】 次の複素数を求めてください.
はじめに「かっこ」を外します.
(1−2i )(3+i )=3+i−6i−2i2 i2を−1に替えます. 3+i−6i+2=5−5i…(答)
はじめに展開公式を使って「かっこ」を外します.
(2−3i )2=4−12i+9i2 i2を−1に替えます. 4−12i−9=−5−12i…(答)
はじめに分母の共役複素数を分母と分子に掛けて,分母を実数にします.
== i2を−1に替えます. =…(答) |
|
■オイラーの公式,ド・モアブルの定理
≪超重要≫
(解説)【指数関数と三角関数の関係:オイラーの公式】 eiθ=cosθ+i sinθ…(1) 
無限級数展開(マクローリン級数展開)を用いると
ex=1+x+++···
sin x=x−+−++···
cos x=1−+−++···
となるので
eix=1+ix+++···
ここで,i2=−1だから
eix=1+ix−−i+···
=(1−+−++···)+i(x−+−++···)
=cos x+i sin x
指数関数と三角関数をつなぐこの公式は「オイラーの公式」と呼ばれます.
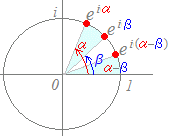
【単位円上の複素数の積→偏角は和になる】
(解説)(cosα+i sinα)(cosβ+i sinβ)=cos(α+β)+i sin(α+β)…(2) 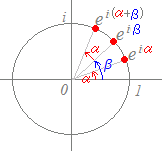 指数法則により
eaeb=ea+b
が成り立つから
eiαeiβ=ei(α+β)
すなわち,次の式が成り立つ.
(cosα+i sinα)(cosβ+i sinβ)=cos(α+β)+i sin(α+β)
【ド・モアブルの定理】
(解説)(cosθ+i sinθ)n=cos(nθ)+i sin(nθ)…(3) 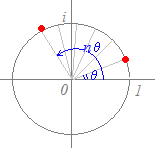
(eiθ)n=einθ
だから
(cosθ+i sinθ)n=cos(nθ)+i sin(nθ)
この関係式はド・モアブルの定理と呼ばれます.
【単位円上の複素数の商→偏角は差になる】
(解説)
=cos(α−β)+i sin(α−β)…(4)
=ea−b
が成り立つから
=ei(α−β)
すなわち,次の式が成り立つ.
=cos(α−β)+i sin(α−β)
|
左の欄では(1)から(2)(3)(4)を示したが,高校では(1)を習わないので(2)(3)(4)は三角関数の変形だけで示します.(現行教育課程では,複素数平面やド・モアブルの定理は登場しません.)
 (2)← (cosα+i sinα)(cosβ+i sinβ) =cosαcosβ+icosαsinβ+isinαcosβ+i2sinαsinβ =(cosαcosβ−sinαsinβ)+i(cosαsinβ+sinαcosβ) ここで三角関数の加法定理を用いると cos(α+β)+i sin(α+β) になる. (3)← (cosθ+isinθ)2=(cosθ+isinθ)(cosθ+isinθ) (2)の結果により =cos(2θ)+isin(2θ)…(*) 次に, (cosθ+isinθ)3=(cosθ+isinθ)2(cosθ+isinθ) 右辺に(*)を使うと (cos(2θ)+isin(2θ))(cosθ+isinθ) さらに,右辺に(2)の結果を使うと cos(3θ)+isin(3θ) 以下,順次示される.[正式には数学的帰納法を使ってまとめる方がよい] (4)←
=
=
分母はcos2β+sin2β=1になるから=cosαcosβ+sinαsinβ+i(sinαcosβ−cosαsinβ) ここで三角関数の加法定理を用いると cos(α−β)+isin(α−β) になる. 【問題7】 次の複素数を求めてください.
偏角の和を求めます.
+= cos+i sin=i…(答)
公式が適用できるように,a+biの形にします.
そのとき,sin(−θ)=−sinθ, cos(−θ)=cosθとなることに注意します. (cos+i sin )(cos(−)+i sin(− )) そこで,偏角の和を求めます. +(− )= cos+i sin=+i…(答)
公式を使って偏角を求めます.
2×= cos+i sin=i…(答)
偏角の差を求めます.
−=−
cos(− )+i sin(− )=−i…(答) |
|
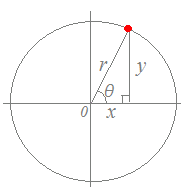
■複素数の極形式
複素数の2通りの表し方
(1) (実部)+i(虚部) の形 (2) 絶対値×(cosθ+i sinθ) の形(←これが極形式)
○右図4のように,半径rの円を描くと
sinθ=
cosθ=
だから
x=rcosθ
になります.y=rsinθ したがって,
x+yi=rcosθ+irsinθ=r(cosθ+isinθ)
という形で書くことができます.○x+yiをr(cosθ+isinθ)に直すときは,
r=
によって,絶対値rを求めることができます.○複素数の絶対値(大きさ)は,その複素数の原点からの距離を表しています. ■複素数の積商の図形的な意味
【複素数の掛け算は回転・拡大】
複素数z1=r1(cosθ1+sinθ1)にz2=r2(cosθ2+sinθ2)を掛けると
z1z2=r1r2(cos(θ1+θ2)+sin(θ1+θ2))
となるので,これらの積は元の複素数z1の大きさr1をr2倍し,偏角θ1にθ2を加えたものになります.このように,偏角θ2,大きさr2の複素数を掛けると,これらで表される角度と大きさだけ「回転と拡大」を行うことになります. 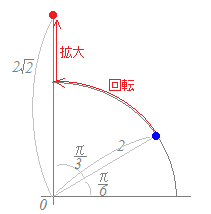 【例1】
【例1】
2(cos+i sin)
は,絶対値が2で偏角がの複素数(青丸)これに
(cos+i sin)
を掛けると,回転して, 倍したものになる(赤丸)
2(cos+i sin)×(cos+i sin)
=2(cos+i sin)=2i
 【例2】
【例2】3=3(cos0+i sin0)は,絶対値が3で偏角が0の複素数(青丸) これに
i=cos+i sinを掛けると,
回転したものになる(赤丸:3i) さらに,iを掛けると,回転したものになる(緑丸:−3) さらに,iを掛けると,回転したものになる(茶丸:−3i) さらに,iを掛けると,回転したものになる(青丸:3)
【複素数の割り算は逆回転・縮小】
複素数z1=r1(cosθ1+sinθ1)をz2=r2(cosθ2+sinθ2)で割ると
==(cos(α−β)+isin(α−β))
←(4)
となるので,この商は元の複素数z1の大きさr1をr2で割り,偏角θ1からθ2を引いたものになります.このように,偏角θ2,大きさr2の複素数で割ると,これらで表される角度と大きさだけ「逆回転と縮小」を行うことになります.  【例1】
【例1】8(cos+i sin)=4+4iは, 絶対値が8で偏角がの複素数(青丸) これを
2(cos+i sin)=2iで割ると,
時計回りに回転して,絶対値を半分にしたものになる.(赤丸:) == ==−2i+2=2−2i さらに,2iで割ると,時計回りに回転して,絶対値を半分にしたものになる. (緑丸:−−i) 【問題8】
(1)次の図において,青で示した点は複素数
z1=2(cos+i sin )
を表しています.もう一つの複素数を
z2=(cos+i sin )
とするとき,これらの積z1z2を次の複素数平面上で示してください. Help
z1,z2の絶対値は各々2,だから
z1z2の絶対値は2×=4
z1,z1の偏角は各々だから
z1z2の偏角は+=
になります.したがって,
z1z2=4(cos+i sin )=4i
をポイントします.
右上に続く→↑
|
図4
 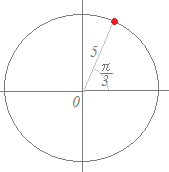 右図の赤で示した点が表す複素数は
右図の赤で示した点が表す複素数は
5(cos+i sin)
=5(+i)
=+i
→続き
(2)次の図において,青で示した点は複素数
z1=2(cos+i sin )
を表しています.もう一つの複素数を
z2=cos−i sin
とするとき,これらの積z1z2を次の複素数平面上で示してください.
Help
sin(−θ)=−sinθ, cos(−θ)=cosθだから
z2=cos(− )+i sin(− )と書ける.
z1,z2の絶対値は各々2,1だから
z1z2の絶対値は2×1=2
z1,z1の偏角は各々, −だから
z1z2の偏角は−=−
になります.したがって,
z1z2=2(cos(− )+i sin(− )=2−2i
をポイントします.
(3)次の図において,赤で示した点は複素数
z1=3(cos+i sin )
を表しています.もう一つの複素数を
z2=3(cos+i sin )
とするとき,これらの商を次の複素数平面上で示してください.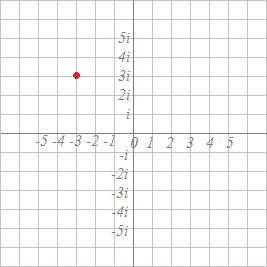
Help
z1,z2の絶対値は各々3,3だから
の絶対値は=
z1,z1の偏角は各々, だから
の偏角は−=
になります.したがって,
=(cos+i sin )=1+i
をポイントします.
(4)次の図において,赤で示した点は複素数
z1=3(cos+i sin )
を表しています.もう一つの複素数を
z2=(cos−i sin )
とするとき,これらの商を次の複素数平面上で示してください.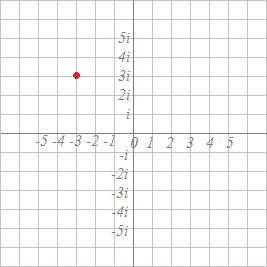
Help
sin(−θ)=−sinθ, cos(−θ)=cosθだから
z2=(cos(− )+i sin(− )と書ける.
z1,z2の絶対値は各々3,だから
の絶対値は=3
z1,z1の偏角は各々, −だから
の偏角は−(− )=
になります.したがって,
=3(cos+i sin )=−3i
をポイントします.
|