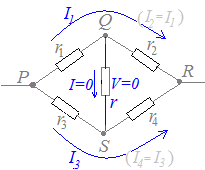
|
右図１のように２つの並列回路の間に橋を渡したような形になっている回路をブリッジ回路といいます．
抵抗を測定する機器を端子間にあてても，測定機器自体にも電流が流れるため必ずしも正確な測定はできません．これに対して，右図１のようなブリッジ回路においてI=0 (V=0)となる平衡条件を満たすとき，あらかじめ分かっている抵抗r1, r2, r3の値からr4の値を正確に測定することができます．このような目的で使われるブリッジ回路をホイートストンブリッジといいます．
【ブリッジ回路の平衡条件】
※ 抵抗rに電流が流れないのは，Q, Sの電位が等しく，電位差V=0となる場合です．右図１のようなブリッジ回路においてQS間に電流が流れない平衡状態にあるとき r1:r2=r3:r4
が成り立つ．
※ r1:r3=r2:r4としてもよい.
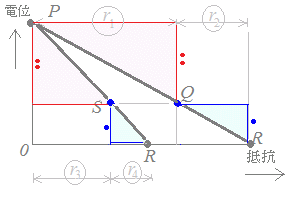
※ 積の形 r1r4=r2r3 で使ってもよい. ≪図による解説≫ 右図２においてr1 : r2=●● : ● これとr3 : r4=●● : ●とが等しければ SとQは同じ高さ（電位）になり，QS間に電流は流れない．
この図は横が抵抗R，縦が電位（電圧）Vになっており，傾きの大きさが電流Iを表す．PQ間とQR間に流れる電流が等しいので，図のPQRは直線になる．同様にしてPSRも直線
≪式による解説≫ V=0, I=0 → r1:r2=r3:r4
図１においてQ, Sの電位が等しく，それらの電位差がV=0のとき，Q, S間には電流は流れないから，I2=I1，I4=I3このとき，PQ間の電圧降下はPS間の電圧降下に等しくなるから I1r1=I3r3…(1) 同様にして，QR間の電圧降下はSR間の電圧降下に等しくなるから I1r2=I3r4…(2) (1)より = (2)より = よって = r1:r3=r2:r4 r1r4=r2r3 r1:r2=r3:r4 →右に続く
|
図１
  →続き r1:r2=r3:r4 → V=0, I=0
r1:r2=r3:r4のとき，まず図１の赤で示した部分がつながっていない状態で考えると，上の(1)のようにPQ，PS間の電圧降下が等しいからV=0, I=0 よって，赤で示した部分をつないでも電流は流れない． |
|
［問題１］
図の直流回路において，200[V]の直流電源から流れ出る電流が25[A]である。16[Ω]とr[Ω]の抵抗の接続点aの電位をVa[V]，8[Ω]とR[Ω]の抵抗の接続点bの電位をVb[V]とする。Va=Vbとなるr[Ω]とR[Ω]の値の組合せとして，正しいものを次の(1)〜(5)のうちから一つ選べ。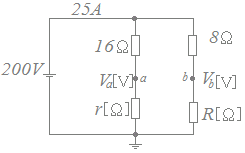 
rR
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験（電験三種）平成23年度「理論」問6 なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする． |
Va=Vbだから
16:r=8:R
r=2R
(3)(4)が条件を満たしているが，未知数がrとRの２つあるから，これだけでは求まらない．200V, 25Aの条件を満たす方を探す．
合成抵抗が=8となるのは，･･･(4)の値で確かめると
==8
→【答】(4)
方程式として解くと少し長くなる：
=8より 128+16R+8r+rR=192+8r+8R rR+8R−64=0 r=2Rを代入 2R2+8R−64=0 R2+4R−32=0 (R+8)(R−4)=0 R=4 (>0) このとき r=2R=8 |
|
［問題２］
図のような，抵抗P=1[kΩ]，抵抗Q=10[Ω]のホイートストンブリッジ回路がある。このブリッジ回路において，抵抗Rは100[Ω]〜2[kΩ]の範囲内にある。このRのすべての範囲でブリッジの平衡条件を満たす可変抵抗Sの値の範囲として，正しいのは次のうちどれか。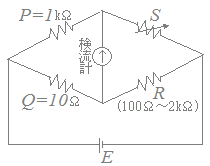 
(1)0.5[Ω]〜10[Ω] (2)10[Ω]〜200[Ω] (3)500[Ω]〜5[kΩ] (4)10[kΩ]〜200[kΩ] (5)500[kΩ]〜1[MΩ] HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験（電験三種）平成14年度「理論」問5 なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする． |
（参考）
1[kΩ]=1,000[Ω]，1[MΩ]=1,000,000[Ω] S:R=1000:10 S=100R ここでR=100〜2000[Ω]のとき S=10,000[Ω]〜200,000[Ω] S=10[kΩ]〜200[kΩ] →【答】(4)
|
|
［問題３］
図のような直流回路において，抵抗3[Ω]の端子間の電圧が1.8[V]であった。このとき，電源電圧E[V]の値として，正しいのは次のうちどれか。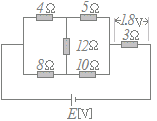 
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験（電験三種）平成16年度「理論」問5 なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする．
4:5=10:8だからブリッジは平衡状態にあり，12[Ω]の抵抗には電流は流れない．
合成抵抗は +3=6+3=9[Ω] 電流は =0.6[A] だから E=0.6×9=5.4[V] →【答】(3)
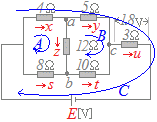右図のように電流x,y,z,s,t,u及び電圧Eを未知数として，未知数7個，方程式7個の連立方程式を立てて解くこともできるが，このように一般的に解くと大変な作業になる．≪大変な作業の例≫ 分岐点a,b,cについて，各々キルヒホフの第１法則を適用すると x=y+z…(1) z+s=t…(2) y+t=u…(3) 閉回路A,B,Cについて，各々キルヒホフの第２法則を適用すると 4x+12z−8s=0…(4) 5y−10t−12z=0…(5) 4x+5y+3u=E…(6) 3[Ω]の抵抗の端子間電圧が1.8[V]だから u=0.6…(7) →右に続く
|
→続き
まず(7)を(6)に代入して未知数6個，方程式6個の連立方程式とし，次に(1)を(4)(6)に代入してxを消去すると未知数5個，方程式5個になる． z+s=t…(8) y+t=0.6…(9) y+4z−2s=0…(10) 5y−10t−12z=0…(11) 9y+4z+1.8=E…(12) (8)を用いてt消去：未知数4個，方程式4個にする y+z+s=0.6…(13) y+4z−2s=0…(14) 5y−2z−10s=0…(15) 9y+4z+1.8=E…(16) (13)×2+(14)，(13)×10+(15)によりs消去：未知数3個，方程式3個にする 3y+6z=1.2…(17) 15y−12z=6…(18) 9y+4z+1.8=E…(19) (17)×2+(18)によりz消去 21y=8.4 y=0.4→z=0→E=5.4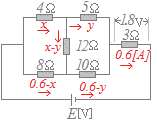 
方程式として解くときでも，分かるものはなるべく数字にし，変数の数を減らす方が解きやすい．閉回路Aについて，々キルヒホフの第２法則を適用すると 4x+12(x−y)−8(0.6−x)=0…(1) 閉回路Bについて，キルヒホフの第２法則を適用すると 5y−10(0.6−y)−12(x−y)=0…(2) (1)→ 24x−12y=4.8 6x−3y=1.2…(3) (2)→ −12x+27y=6 −4x+9y=2…(4) (3)×3+(4) 14x=5.6 x=0.4 (3)に代入 −3y=−1.2 y=0.4 このとき E=4x+5y+1.8=1.6+2.0+1.8=5.4 |
|
［問題４］
図のブリッジ回路を用いて，未知抵抗Rxを測定したい。抵抗R1=3[kΩ]，R2=2[kΩ]，R4=3[kΩ]とし，R3=6[kΩ]の滑り抵抗器の接触子の接点Cをちょうど中央に調整したとき（Rac=Rbc=3[kΩ]）ブリッジが平衡したという。次の(a)及び(b)に答えよ。 ただし，直流電圧源は6[V]とし，電流計の内部抵抗は無視できるものとする。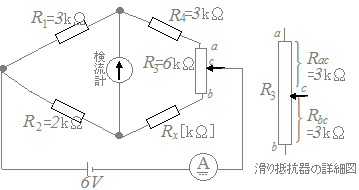 
(a) 未知抵抗Rxの値として，正しいのは次のうちどれか。 (b) 平衡時の電流計の指示値[mA]の値として，最も近いのは次のうちどれか。
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験（電験三種）平成18年度「理論」問16 なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする． |
R4+Rac=3+3=6，Rx+Rbc=Rx+3だから､平衡状態のとき
3:6=2:(Rx+3) 12=3(Rx+3) 4=Rx+3 Rx=1 →【答】(a)--(3)
Rx=1のとき，
3[kΩ]，3[kΩ]，3[kΩ]の直列接続からなる9[kΩ] 2[kΩ]，1[kΩ]，3[kΩ]の直列接続からなる6[kΩ] の抵抗が並列接続されていることになるから，全体の合成抵抗は =3.6[kΩ]=3.6×103[Ω] I==1.7×10−3[A]=1.7[mA] →【答】(b)--(4)
|
|
［問題５］
図のような直流回路において，スイッチSを閉じても，開いて も電流計の指示値は，[A]一定である。このとき，抵抗R3 [Ω]，R4[Ω]のうち小さい方の抵抗[Ω]の値として，正しいのは次のうちどれか． ただし，直流電圧源はE[V]とし，電流計の内部抵抗は無視できるものとする。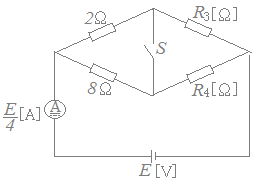 
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験（電験三種）平成19年度「理論」問6 なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする．
ホイートストンブリッジの平衡条件を満たしていれば，Sの両端には電圧が加わっておらず，Sを閉じても，開いても「回路の外周の電流は変化しない」(*)はずである．
平衡条件は2:R3=8:R4 2R4=8R3 R4=4R3…(1) （電流）==の関係から，全体の抵抗は4[Ω]になるはずだから =4 =4 =4 4(2+R3)=20 2+R3=5 R3=3 →【答】(3)
試験においては，限られた時間内に答案を作成しなければならないという最優先の事情があるので，問題を一般的に解くよりも，その問題の特殊事情につけこんでなるべく簡単な方法で解く方がよい．特に，選択問題においては「答はただ一つしかない」はずなので，条件に合うものを見つけたらそれが答になる．だから，上のように「なるべく簡単な方法で解く」のがよい．
しかし，ここではあえて参考として，他に解がないかどうか調べてみる． 上の解き方において，平衡状態にあれば「回路の外周の電流は変化しない」(*)ことは言えるが，「回路の外周の電流は変化しない」のは平衡状態にあるときに限ると一般的に言えるかどうか．少なくとも教科書的常識とは言い切れない．そこで，スイッチSを閉じても，開いても「回路の外周の電流は変化しない」という条件を使って解いてみる． →右に続く
|
→続き
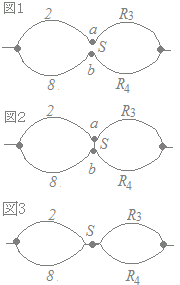右図１のような回路において，端子a, b間に電圧がかかっているときにスイッチSを閉じて，図２のように，すなわち図３のようにするとどうなるのかと考えるのは嫌な問題になる．そもそも，スイッチSには抵抗が入っていないため，ショートさせてしまうことになり，（少なくとも過渡的には）大電流が流れることとなり，大変まずいことになる．I=において R→0ならI→∞ そこで，図３のような「並列接続の直列接続」での電流と図１のような「直列接続の並列接続」での電流を別々に調べて，これらを比較することにする． 図３においては，左半分の合成抵抗は1.6[Ω]で，全体の合成抵抗は4[Ω]だから，右半分の合成抵抗は2.4[Ω]になる． =2.4…(1) 図１においては，上半分の合成抵抗は2+R3[Ω]で下半分の合成抵抗は8+R4[Ω]で，全体の合成抵抗は4[Ω]だから =4…(2) (1)→ R3R4=2.4R3+2.4R4…(1’) (2)→ (2+R3)(8+R4)=4(10+R3+R4) 16+2R4+8R3+R3R4=40+4R3+4R4 R3R4=2R4−4R3+24…(2’) (1’)−(2’) 0=6.4R3+0.4R4−24 0=16R3+R4−60 R4=60−16R3…(3) (3)を(2’)に代入 R3(60−16R3)=2(60−16R3)−4R3+24 60R3−16R32=120−32R3−4R3+24 16R32−96R3+144=0 R32−6R3+9=0 (R3−3)2=0 R3=3 このとき(3)より R4=60−48=12 小さい方は R3=3 →【答】(3)
|
|
（平衡でない場合）
［問題６］
図の直流回路において，次の(a)及び(b)に答えよ。 ただし，直流電圧E[V]の値は一定で変化しないものとする。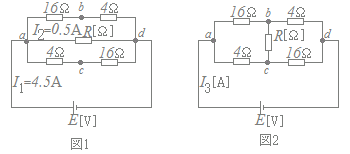 
(a) 図１のように抵抗R[Ω]を端子a, d間に接続したとき，I1=4.5[A]，I2=0.5[A]の電流が流れた。抵抗R[Ω]の値として，正しいのは次のうちどれか。 (b)図１の抵抗R[Ω]を図２のように端子b, c間に接続し直したとき，回路に流れる電流I3[A]の値として，最も近いのは次のうちどれか。
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験（電験三種）平成17年度「理論」B問題 問7 なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする．
図１では上の経路も下の経路も20[Ω]の抵抗になっており，bとcに流れる電流は等しく，それらの合計は4.5−0.5=4.0[A]だから，bとcには各々2.0[A]の電流が流れている．
したがって，a, d間の電圧は 2.0×20=40[V](=E) R==80 →【答】(3)
|
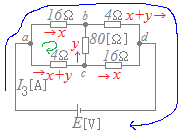右図においてa, dの左右を逆にしても抵抗の組合せは同じになるから，16[Ω]，4[Ω]の抵抗に流れる電流は各々等しい．
なるべく未知数の個数が少なくなるように，4[Ω]の抵抗に流れる電流は，キルヒホフの第１法則を使ってx+yと表しておく．
青線で示した閉回路についてキルヒホフの第２法則を適用すると16x+4(x+y)=40 16x+4x+4y=40 20x+4y=40 5x+y=10…(1) 緑線で示した閉回路についてキルヒホフの第２法則を適用すると 16x−80y−4(x+y)=0 16x−80y−4x−4y=0 12x−84y=0 x=7y…(2) (2)を(1)に代入すると 35y+y=10 36y=10 y=0.28 これを(2)に代入 x=1.96 ゆえに I3=x+(x+y)=2x+y=3.92+0.28=4.2 →【答】(2)
|
...メニューに戻る