■電流が作る磁界
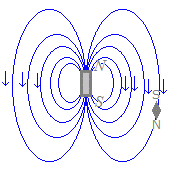
○　磁力線はN極から出て，S極に入るように描く．

○　右図のように，大きな磁石が作る磁界の中に（向きが自由に変わる）小磁針を置くと，小磁針のN極は磁力線の向きに向く．
■アンペアの右ねじの法則
　電流が流れると磁界が発生します．右図１のように電流の向きを「右ねじの進む方向」とするとき，磁界の向きは「ねじの回転する方向」になります．これを発見者の名前をとって「アンペアの右ねじの法則」と言います．

　図２の左の図のような長い直線状の導線にこちらからあちらに向かって電流が流れているとき，右巻きの同心円状の磁界が発生することが，アンペアの法則からいえます．
（磁界の強さは，導線からの距離に関係しており［後出］，導線からの距離が等しい点では磁界の強さは同じになります．だから，同心円の上では磁界は同じ強さになります．）

　導線の断面を描くときに，図２の右側の図のように，電流が向こう向きに流れているときは，プラスねじの頭を見たときのイメージでの記号で表し，電流がこちら向きに流れているときは，ねじのとがっている方から見たときのイメージでの記号で表されます．

　具体的に与えられた電流と導線の形から個々の点に生ずる電界の強さは，小さな導線素片が作る磁界に関するビオ・サバールの法則（電流の強さI，半径r，導線となす角θによって決まる）
ΔH=sinθΔl
を使って積分計算によって求めることができるが，実際の試験問題では個別に積分計算をしていると大変なので，積分計算から分かっている次の結果を使う．

(1)　アンペアの周回路の法則
右図４のように，磁界の強さが一定H[A/m]のところを一周したときの経路の長さをl[m]とするとき，
Hl=I が成り立つ．
(2)　直線電流による磁界
右図５のように，無限に伸びている直線状の導体にI[A]の電流が流れているとき，この導体からr[m]離れた点における磁界の強さは
H=[A/m]
（円の一周が2πr[m]で，この円周上ではどの点も条件が同じだから磁界は等しく，(1)によりH×2πr=Iが成り立つ．）
(3)　円形電流が円の中心に作る磁界
右図６のような半径r[m]の円形電流にI[A]の電流が流れているとき，この円の中心における磁界の強さは
H=[A/m]
「磁界の向き」は，アンペアの右ねじの法則を円周上の２，３の点に当てはめてみると分かる．
（この磁界の向きについても，新たに右ねじの法則を考える立場もあるが，公式は確実に使えるものに絞る方がよく，１つの右ねじの法則だけですぐに分かる．）

（この式は(2)の式と似ているが，全く異なる式であることに注意．この公式で求められるのは，円の中心の磁界だけで他の点（中心から少しずれた位置や円の中心を通る直線上の他の点）の磁界はこの公式からは求められない．右図○印の箇所のみ分かり，×印の付いている箇所についてはこの公式では求められない．）
ビオ・サバールの法則から，右図Δlの導線素片が作る磁界が（θ=90° → sinθ=1）
ΔH=Δl
になることから
=（Δlの場所に関係なく一定）
H=dl=×2πr=
(4) ｎ巻きコイルの中心にできる磁界
右図７のようなｎ回巻かれたコイルでは，電流がnI[A]の円形電流と考えればよいから，
H=[A/m]
図７　［ｎ巻きコイルの中心にできる磁界］
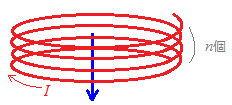図１
図２
図３
図４　［アンペアの周回路の法則］




図５　［直線電流による磁界］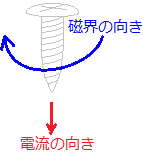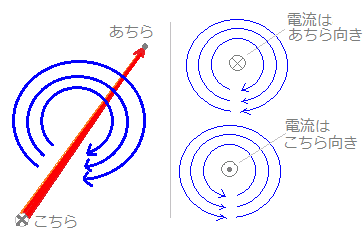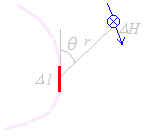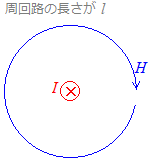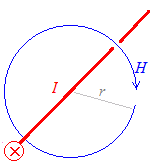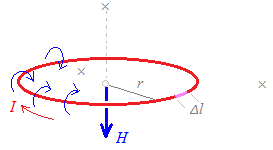
図６　［円形電流が円の中心に作る磁界］


※公式(2)(3)の違い…危険な落とし穴
［問題１］
無限に長い直線状導体に直流電流を流すと，導体の周りに磁界が生じる。この磁界中に小磁針を置くと，小磁針の（ア）は磁界の向きを指して静止する。そこで，小磁針を磁界の向きに沿って少しずつ動かしていくと，導体を中心とした（イ）の線が得られる。この線に沿って磁界の向きに矢印をつけたものを（ウ）という。
また，磁界の強さを調べてみると，電流の大きさに比例し，導体からの（エ）に反比例している。
上記の記述中の空白箇所（ア），（イ），（ウ）及び（エ）に記入する語句として，正しいものを組み合わせたのは次のうちどれか。

（ア）（イ）（ウ）（エ）



　一般財団法人電気技術者試験センターが作成した問題
　第三種電気主任技術者試験（電験三種）平成17年度「理論」問3
　なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする．
［問題２］
図のように，A，B２本の平行な直線導体があり，導体Aには1.2[A]の，導体Bにはそれと反対方向に3[A]の電流が流れている。導体AとBの間隔がl[m]のとき，導体Aより0.3[m]離れた点Pにおける合成磁界が零になった。l[m]の値として，正しいのは次のうちどれか。
ただし，導体A，Bは無限遠とし，点Pは導体A，Bを含む平面上にあるものとする。

(1)0.24 (2)0.45 (3)0.54 (4)0.75 (5)1.05


　一般財団法人電気技術者試験センターが作成した問題
　第三種電気主任技術者試験（電験三種）平成15年度「理論」問3
　なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする．
［問題３］
図１のように，無限に長い直線状導体Aに直流電流I1[A]が流れているとき，この導体からa[m]離れた点Pでの磁界の大きさはH1[A/m]であった。
一方，図２のように半径a[m]の一巻きの円形コイルBに直流電流I2[A]が流れているとき，この円の中心点Oでの磁界の大きさはH2[A/m]であった。
H1=H2であるときのI1とI2の関係を表す式として，正しいのは次のうちどれか。

(1)I1=π2I2 (2)I1=πI2 (3)I1=
(4)I1= (5)I1=I2



　一般財団法人電気技術者試験センターが作成した問題
　第三種電気主任技術者試験（電験三種）平成19年度「理論」Ａ問題 問1
　なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする．
［問題４］
図のように，点Oを中心とするそれぞれ半径1[m]と半径2[m]の円形導線のと，それらを連結する直線状の導線からなる扇形導線がある。この導線に，図に示す向きに直流電流I=8[A]を流した場合，点Oにおける磁界[A/m]の大きさとして，正しいのは次のうちどれか。
ただし，扇形導線は同一平面上にあり，その巻数は一巻きである。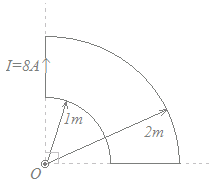

(1)0.25 (2)0.5 (3)0.75 (4)1.0 (5)2.0


　一般財団法人電気技術者試験センターが作成した問題
　第三種電気主任技術者試験（電験三種）平成21年度「理論」問4
　なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする．
［問題５］
図１のように，１辺の長さがa[m]の正方形のコイル（巻数：１）に直流電流I[A]が流れているときの中心点O1の磁界の大きさをH1[A/m]とする。また，図２のように，直径[m]の円形コイル（巻数：１）に直流電流I[A]が流れているときの中心点O2の磁界の大きさをH2[A/m]とする。このとき，磁界の大きさの比の値として，最も近いものを次の(1)〜(5)のうちから一つ選べ。
ただし，中心点O1，O2はそれぞれ正方形のコイル，円形のコイルと同一平面上にあるものとする。
参考までに，図３のように，長さa[m]の直線導体に直流電流I[A]が流れているとき，導体から距離r[m]離れた点Pにおける磁界の大きさH[A/m]は，H=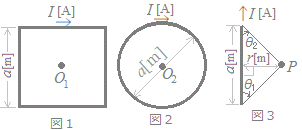(cosθ1+cosθ2)で求められる（角度θ1とθ2の定義は図参照）。

(1)0.45 (2)0.90 (3)1.00 (4)1.11 (5)2.22


　一般財団法人電気技術者試験センターが作成した問題
　第三種電気主任技術者試験（電験三種）平成23年度「理論」問4
　なお，問題及び解説に対する質問等は，電気技術者試験センターに対してでなく，引用しているこのホームページの作者に対して行うものとする．
.