|
【交流とは】
【用語】電池によって電圧・電流が生ずる場合のように一定方向に一定の電圧がかかっているときの電圧や電流を直流といいます.これに対して電圧や電流の向きが交互に変化するものを交流といいます. 交流のうちで最もよく登場するのが正弦波交流で y=asin(ωt)
の形をしています.
○ 正弦曲線…下図のように半径がr,OPの基準線(横軸)からのずれの角(反時計回りに測定する=左回り)をθとするとき,円周上の1点のx座標とy座標は
y=rsinθ
x=rcosθ
で表されます.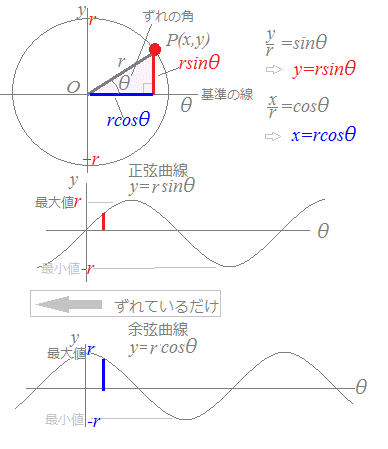 
○ 正弦波…上で述べたように正弦曲線と余弦曲線は横にずれているだけのものです.そこで,交流を表す場合には,通常,正弦波と呼び,余弦波という言い方はしません.
画像圧縮技術のJPEGにおいては,もっぱらcosnθが使われます.このように,分野によって,正弦と余弦のどちらが好まれるかは変わります.
○ 位相,最大値(振幅)
 y=rsinθ(r>0)において,θを変化させると,θ=90°, 90°+360°,...のとき,yは最大値y=rをとります.(sin90°=1だから) この最大値は円の図では円の半径に対応しており,正弦曲線では山の高さ(振幅)に対応しています.(山の高さというのは原点[中腹]から見たときの山の高さのことで,谷から山までの高さではありません.谷から山まで測ったものは直径に対応しており2rになります.)
y=rcosθ(r>0)においては,θを変化させると,
θ=0°, 360°,...のとき,最大値y=rとなります(cos0°=1だから)が,上で述べたように,交流を扱うときは正弦波交流だけに絞って考えればよい. 交流理論では上記の最大値をrの代わりにa (a>0)で表すことが多く,
y=a sinθの式がよく使われます.
○ 角度の単位ラジアン…角度の単位としては60分法[度数法](円の1周を360°とし,1度=60分,1分=60秒とする)と弧度法(円周上で半径の長さrに等しい円弧となるような中心角を1弧度[1ラジアン]とする).度で表されているときは数字に°を付け,ラジアンで表されているときは,何も付けない.(明示的に書くときはラジアン,radなどと書く.)
1ラジアンの角は1°と比較するととても大きく,1ラジアン=約57°になります.(3.14..ラジアンが180°) 60分法[度数法]で測った角度と弧度法[ラジアン]で測った角度とは次の表1のように対応します.覚えなければならないのは 180°=π(ラジアン)
だけで,他の度θをラジアンxに直す(ラジアンxを度θに直す)には次の比例計算で求めることができます.
x:π=θ°:180°
表1
例 90°を弧度法に直すには? → x:π=90°:180° 180x=90
x=
|
○ 角速度ω…ωはギリシャ文字Ωの小文字でオメガと読む.アルファベットのwではない.
時間の経過に沿って,位相が変化して行くときに,1秒当たりに進む角度を各速度といいωで表します.1秒でωラジアンだからt秒でθ=ωtラジアンになります. 正弦波を時間t(秒)の関数として表すと, y=asin(ωt)
になります.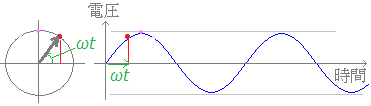 ○ 角速度,周波数,周期の関係
1秒間に同じ波形(山から山,谷から谷,登りの中腹から登りの中腹)を繰り返す回数を周波数といいf[Hz](ヘルツ)で表します.1周すると角度は2πラジアンだから,f回で2πfラジアンになります. ω=2πf
1周するに要する時間を周期といいT[s](秒)で表します.1秒当たりf回なら,1周するに要する時間は
T=
各速度ωで(1周するに要する時間)T[s](秒)だけ進むと,ちょうど1周するので
ωT=2π
○ 「遅れている」と「進んでいる」
y=asin(θ−α)の位相θ−αは,y=asin(θ)の位相θに対して,αだけ「遅れている」といいます. y=asin(θ+α)の位相θ+αは,y=asin(θ)の位相θに対して,αだけ「進んでいる」といいます.
式では遅れている(−),進んでいる(+)は見た目の通りです.
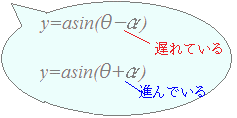
これに対して,グラフで「進んでいる」か「遅れている」かを判断するときは,逆に見えてしまうことがあるので注意が必要です. 次の図3において(ア)(イ)(ウ)の同じ記号●▲■◆...に注意すると,
(ア)は(イ)よりも「遅れています」
【例】(ウ)は(イ)よりも「進んでいます」
(イ)ではθ=0のときy=0ですが(●印:山の登りの中腹),(ア)ではθ=0のときyはまだ負の値になっており,θ=αになってからようやくy=0になります.
(ウ)ではθが負の値のときにすでにy=0になっており,θ=0のときにはy=a sinαという進んだ値となっています. ⇒ このように,グラフを右に移動すると位相θは「遅れる」ことになり,左に移動すると位相θは「進む」ことになります. 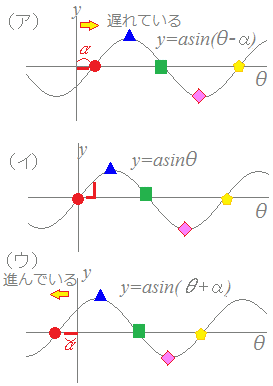 ○ 時間単位で見たときの位相の遅れ,進み
位相に関して言えば,y=asin(ωt−θ)は,y=asin(ωt)よりも位相がθだけ「遅れて」います. 逆に,y=asin(ωt+θ)は,y=asin(ωt)よりも位相がθだけ「進んで」います. しかし,時間に関して言えばy=a sin(ωt−θ)=a sin ω(t−) はy=asin(ωt)をt方向にだけ平行移動したもの になっており,秒遅れています. 同様にして,y=a sin(ωt+θ)=a sin ω(t+) はy=asin(ωt)をt方向に−だけ平行移動したもの になっており,秒進んでいます.  (1) y=2sin(3t−π)のグラフはy=2sin(3t)のグラフよりも
秒遅れています.
(振幅[最大値]の2は遅れには影響しません)
(2) y=3sin(2πt+π)のグラフはy=3sin(2πt)のグラフよりも
=0.5秒進んでいます.
(振幅[最大値]の3は進みには影響しません)
ω=2π ⇒ ωT=2πよりT=1 1周期が1秒の波において,その半回転(πラジアン)だけ進んでいるのだから,0.5秒進んでいます. |
||||||||||||||||||||||
|
位相差は
(100πt+)−(100πt+)=[rad]
角速度は100π[rad/s]だから,時間で測れば
=[s]
→【答】(3)
|
|||||||||||||||||||||||
|
4sin120πt=4 (t>0)よりsin120πt=
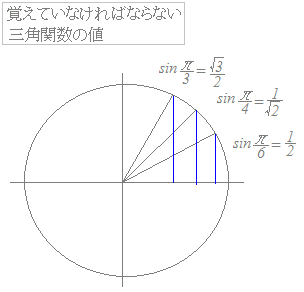 →【答】(1)
|
|
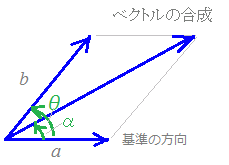
【周波数が等しい交流電圧の合成】
右図1のように回路に2種類の交流電源
E1=a sinωt
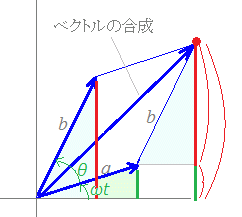
が加わっているとき,回路に加わる合成電圧のの振幅[最大値]と位相は右図2のようなベクトル図で求めることができます.E2=b sin(ωt+θ) 時刻tが変化していくと,元のベクトルは2つとも左回りにまわりますが,相対的にE2=b sin(ωt+θ)の方がθだけ進んでいるという関係は変わらないので,右図3のようにE1=a sinωtの方を基準の方向として,それよりもどれだけ進んでいるか(α)と最大値[振幅]:図の合成したベクトルの長さを求めればよいと考えます.
この公式そのものは,高校の数学の教科書にはありません.
(解説)高校の教科書では,和を積に直す公式として
sinA+sinB, sinA−sinB
cosA+cosB, cosA−cosB ⇒ 振幅[最大値]と関数の種類(sin, cos)が同じで角度は異なるもの 三角関数の合成公式として
asinθ+bcosθ
しかし,振幅[最大値]も位相も異なる正弦関数を一般的に合成する公式は高校数学では扱っていません.
⇒ 角度が同じでsin, cosの組になっており,振幅[最大値]が異なるもの ただし,cosθ=sin(θ+)だから asinθ+bsin(θ+)すなわち,位相がだけ異なる場合)は,合成できます. y=a sinωtは,図2の緑色で示した直角三角形(斜辺の長さがa)の縦の長さになり,緑で示した線の長さになります. y=b sin(ωt+θ)は,図2の水色で示した直角三角形(斜辺の長さがb)の縦の長さになり,赤で示した線の長さになります. 水色の直角三角形を平行移動すると,赤線の長さ+緑線の長さは図3のように平行四辺形の対角線で作られる直角三角形の縦の長さになります.
合成してできるベクトルの長さやE1となす角は余弦定理を使えばa, b, θで表すこともできますが,かなり複雑な式になり,一般的に数式変形として求めることは要求されません.ここでは「ベクトルの図を描いて求められたらよい」と考えます.
【例題1】
(解説)回路に二つの正弦波交流電源
E1=2 sin ωt[V]
が直列に接続されているとき,合成電圧の最大値を求めよ.またその位相はE1を基準として何[rad]進んでいるか.E2=2 sin(ωt+)[V] 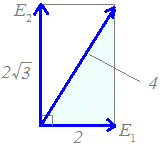 E2の位相はだけ進んでいるから,右図において斜辺方向のベクトルが合成電圧になる.
E2の位相はだけ進んでいるから,右図において斜辺方向のベクトルが合成電圧になる.三平方の定理(ピタゴラスの定理)により斜辺の長さは
===4
したがって,合成電圧の最大値は4[V]また,辺の長さの比が1:2:だから,1つの角が60°=[rad]の直角三角形になっており,位相は[rad]進んでいる. |
図1
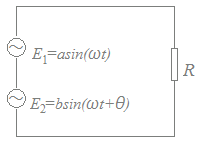  
【例題2】
(解説)回路に三つの正弦波交流電源
E1=100 sin ωt[V]
が直列に接続されているとき,合成電圧の最大値を求めよ.またその位相はE1を基準として何[rad]進んでいるか.E2=200 sin(ωt+)[V] E3=100 sin(ωt−)[V] 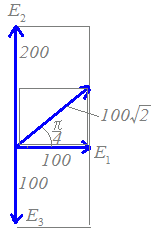 右図のベクトルの和を求める.
右図のベクトルの和を求める.まず,E2とE3は縦方向で,それらの和は上向きに100[V]となるから,全体の和は図のように一辺の長さが100の正方形の対角線の向きになる. 最大値は100[V] 位相はE1よりも[rad]進んでいる. |
|
[問題3]
図のように,二つの正弦波交流電圧源e1[V],e2[V]が直列に接続されている回路において,合成電圧v[V]の最大値はe1の最大値の(ア)倍となり,その位相はe1を基準として(イ)[rad]の(ウ)となる。
上記の記述中の空白箇所(ア),(イ)及び(ウ)に当てはまる語句,式又は数値として,正しいものを組み合わせたのは次のうちどれか。 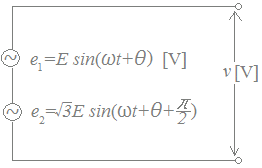
(ア)(イ)(ウ)
HELP
一般財団法人電気技術者試験センターが作成した問題
第三種電気主任技術者試験(電験三種)平成18年度「理論」8 なお,問題及び解説に対する質問等は,電気技術者試験センターに対してでなく,引用しているこのホームページの作者に対して行うものとする. |
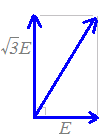 e2はe1よりも進んでいるから,
e2はe1よりも進んでいるから,次のような図によって合成できる.(e1の向きを基準として右向きに固定して表す.) このとき合成電圧の最大値(右図の対角線の長さ)は三平方の定理を使って求めることができ,
==2E
したがって,e1の最大値Eの2倍になる.辺の長さの比がE:2E:E=1:2:の直角三角形になるから,位相は 進んでいる. →【答】(5)
|