← PC�p�͕ʕ�
|
=== �ǎ҂��z�F��ύX�������ꍇ ===
���O���̐F��ς���ɂ́C���̐F���N���b�N
�s�̌��E���僌�x���t
== R�̕���ƃ��[�v == R version 4.0.3, 4.0.4Patched ----- �ŏI�X�V�N����:2021.4.23
�@���̋��ނ́C�̌��E����̃��x���ŁC30������1���ԂقǂŁu��������������v���Ƃ�ڎw���D
R�@����ƃ��[�v
1.�@�v���O���~���O���ꂲ�Ƃ̓���
�@�ȉ��ɂ����ẮC�����u���b�N�̎n�܂�ƏI����\�������ʁi�g���ʁC�u���[�X�C�u���P�b�g�C���Ȃ킿 { �� }�j�̂��Ƃ��C�P�ɒ����ʂƌĂԂ��Ƃɂ���D1.1�@�b�����javascript
�@�b�����javascript�ł́Cif���Cfor���[�v�C����`�ɂ����āC�����ʂ͈�A�̋L���Ƃ��Đ����������ɂ���悭�C�����ʒu�i�s�ƃJ�����j�̓v���O���}�[�̎��R�ł���D�������C�ǂ݂₷�����邽�߂ɐ��������X�^�C���͂���D�@C����̋��ȏ����������J�[�j�n��&���b�`�[�̃X�^�C���ł́C
(1) �u���b�N�J�n�̒����� { ��if��for�Ɠ����s�ɏ���
(2) �u���b�N���̕����^�u�L�[�Ŏ��������� (3) �u���b�N�I���̒����� } ��if��for�̐擪�ʒu�Ɠ����J�����i���ʒu�j�ɏ��� if (����) { ��1; ��2; } ---------- for (����) { ��1; ��2; }�@����ɑ��āCBSD/�I�[���}���̃X�^�C���ł́C�u���b�N�J�n�̒����� { ���u���b�N�I���̒����� } �Ɠ����J�����i���ʒu�j�ɏ����D���G�ȍ\���ɂȂ��Ă���Ƃ��ɁC���₷���̂ŁC���̋��ނ̍�ҁi���j�́C�قƂ�ǂ��̃X�^�C���ŏ����Ă���D for (����) { if (����) { ��1; ��2; } else { ��3; ��4; } } 1.2�@Python
�@Python�ł́C�����ʂ��g�킸�ɁC�_���I�ȊW�̓^�u���g�����������ɂ���ĕ\���D
if ����1:
for �ϐ�1 in �͈�1:
if ����2:
��1
if ����3:
��2
��3
else:
for �ϐ�2 in �͈�2:
if ����4
��4
1.3�@R
�@R��if���Cfor���[�v�C����`�������Ƃ��̒����ʂ̏������́C"�ق�"C�ɂ�����J�[�j�n��&���b�`�[�̃X�^�C�����Ǝv���悢�D�i�P���̏ꍇ�ɂ́C�����ʂ��ȗ��ł��邪�C�u�F�X�ȏꍇ������܂��v�Ɗo��������C���߂̂����͊m���ɂł�����@�����ɒP�������������悢�ƍl������j�D�ڂ����́C���̍��ŏq�ׂ�D
|
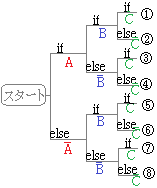
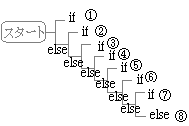
 if (����)
if (����)  �@while�ł́C�E�}�̂悤�ɁC�u���b�N���ɏ����ꂽ�������s����܂łɏ�������������Ă��邩�ۂ����e�X�g���āC���������藧�ꍇ�ɂ����������s����D���������藧���Ȃ��ꍇ�́C���[�v���o�Ď��̗���ɓ���D
�@while�ł́C�E�}�̂悤�ɁC�u���b�N���ɏ����ꂽ�������s����܂łɏ�������������Ă��邩�ۂ����e�X�g���āC���������藧�ꍇ�ɂ����������s����D���������藧���Ȃ��ꍇ�́C���[�v���o�Ď��̗���ɓ���D
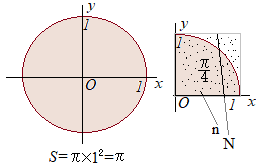 �@���_�𒆐S�Ƃ��锼�a1�̉~�̖ʐς́C
�@���_�𒆐S�Ƃ��锼�a1�̉~�̖ʐς́C