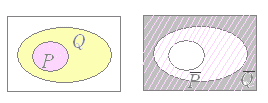
○ 条件とは
x>0 のようにそれだけでは真偽が定まらず,変数 x の値を具体的に定めれば真偽が定まる命題となるものを変数 x に関する条件という.
変数を含んでいるのでこれらを p(x) , q(x) などで表わすとき, p(x) , q(x) それ自体は条件であって真偽は定まらない.(同様にして, , , p(x) かつ q(x) , p(x) または q(x) なども条件となり,これらも真偽は定まらない.)
○ p(x) , q(x) が条件のときでも,「すべての x について p(x) が成立する」という主張は命題になる.
「すべての x について,ある条件 p(x) が成立する.」という主張や,「ある x について,ある条件 p(x) が成立する.」という主張は真偽の定まる命題となる.
一般に,条件 p(x) に対して,「すべての x について 〜 」「ある x について 〜 」などを付け足したものは命題となる.(右の例3,例4)
○ p(x) → q(x) は,「すべての x について( p(x) → q(x) ) 」の省略形なので,命題になる.
「すべての x について,( p(x) → q(x) )」という形のものは命題で,真偽の定まるものとなる.
【重要】
「すべての x について,( p(x) → q(x) )」は,単に
p(x) → q(x) と略されるので,p(x) → q(x) は命題となる.
例えば,「 x>3 → x>1 」は,「すべての x について,(x>3 → x>1 )」の省略である.
※この項目を初めて学ぶときは,(x>3 が成立するようなすべての x について x>1 が成立する )と考えたくなるが,実は x>3 が成立しようがしまいが関係なく,「すべての x について」成立するので,この位置に書いて,
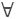 x ( x>3 → x>1 )
の形でよい. x ( x>3 → x>1 )
の形でよい.
(→右参照) x の値に応じて真偽を調べてみると例1で述べたように,仮定が偽であれば結論は何でもよい.条件としての考え方は以下に述べる.) |
例1
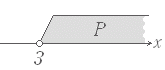
x>0 を条件 p(x) で表わすとき,
x=2 のときは p(x) は真,x= - 1 のときは p(x) は偽となる.
例2
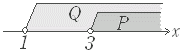
x>0 を条件 p(x) で,x<3 を条件 q(x) で表わすとき,「 p(x) かつ q(x) 」も条件となり,それ自体では真偽は定まらないが,
x=2 のときは 「 p(x) かつ q(x) 」は真,x=4 のときは 「 p(x) かつ q(x) 」は偽となる.
例3
x>0 は条件であってそのままでは真偽は定まらないが,
「すべての x について x>0 が成立する」
⇔ すべての x について x>0
⇔ All x ( x>0 )
⇔ 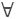 x ( x>0 ) x ( x>0 )
という主張は,本当にすべての x について x>0 が成立すれば真となり,1つでも成立しない x が存在すれば偽となるので命題である.(上の命題は, x= - 2 などのとき成立しないから偽の命題である.)
例4
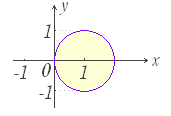
x2 - 2x - 3<0 は条件であってそのままでは真偽は定まらないが,
「ある x について x2 - 2x - 3<0 が成立する」
⇔ ある x が存在して x2 - 2x - 3<0 が成り立つ
⇔ Exist x ( x2 - 2x - 3<0 )
⇔ 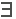 x ( x2 - 2x - 3<0 ) x ( x2 - 2x - 3<0 )
という主張は,本当に1つでも x2 - 2x - 3<0 が成立するような x の値が存在すれば真で,どんな x を持ってきても x2 - 2x - 3<0 が成り立たなければ,これは偽となるから命題である.( x=0 のとき x2 - 2x - 3<0 となるから,これは真の命題となる. )
 x ( x>3 → x>1 )の真偽 x ( x>3 → x>1 )の真偽
| x>3 |
x>1 |
|
x>3 → x>1 |
| p(x) の真理値 |
q(x) の真理値 |
x の例 |
p(x) → q(x) の真理値 |
| 1 |
1 |
x=4 |
1 |
| 1 |
0 |
このような x の値はない |
0 |
| 0 |
1 |
x=2 |
1 |
| 0 |
0 |
x=0 |
1 |
上の表から分かるように,「 p(x) の真理値が1で,q(x) の真理値が0 」となるような x の値は存在しないので,「すべての x の値について」,p(x) → q(x) が成り立っている.
|