|
�y�ϐ������`�̔����������Ƃ́z
�ϐ������`�̔����������Ƃ� y’=f(x)g(y)��������=f(x)g(y) �̂悤�ɁCy’��x, y�̊��̐ςŕ\�������̂������܂��D �y�ϐ������`�̔����������̉������z �ϐ������`�̔����������� =f(x)dx  =f(x)dx �̂悤�ɕό`����Έ�ʉ������߂��܂��D
�y��P�z
�i����E�j����������=y�̈�ʉ������߂Ă��������D ���ӂ�dx���|���Cy�Ŋ����� =dx …(1) �ƕό`���܂��D  ���ӂ�ϕ������ =dx …(2)  log|y|=x+A …(3)  |y|=ex+A=eAex …(4)  eA��B(>0)�Ƃ����� |y|=Bex  y=±Bex  ±B��C(≠0)�Ƃ����� y=Cex (C≠0) …(5)
�i���Z�j
�ȏ�ɂ��Cy=Cex (C�͔C�ӂ̎���) …(��)(5)�����̔����������ɑ������ƁC�i���Ӂj=Cex=�i�E�Ӂj�ƂȂ��Đ�������D (5)�ɂ�����C=0�̂Ƃ���y=0�ƂȂ��āC���̏ꍇ�����̔��������������D 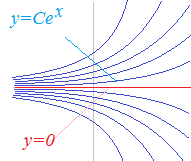 �i(1)(2)���ڂ��������y=0�̂Ƃ��͓r���o�߂ɖ�肪����悤�Ɍ����邪�C���̔�����������p�������Z�ł�y=0�ł��\��Ȃ��D�����������ł͂��̂悤�Ȃ��Ƃ��悭����D�j |
�i�Q�l�j (1)�ɂ���
�@���w�U�Ŕ������ŏ��ɏK���Ƃ��ɁC���O�����W�F�����̔����L��y’��������f ’(x)�ƕ��ׂă��C�v�j�b�c�����̔����L��
���K���D���̂Ƃ��ɏ��S�҂������_����
=
�̂悤�Ȍv�Z�����Ȃ��悤�ɁC�u���̋L���͑S�̂łP�̋L���v�Łu�Ȃǂ��Ă͂����Ȃ��v�Ƌ����܂��D�i�{�j�����̘b��(1)�̕ό`�ł͂ǂ��Ȃ��Ă���̂����Ƌ^��������邱�Ƃ����邩������܂���D
�ጋ�_���猾����
d��������悤�ȕό`�̓_���ł����Cdx��dy���|������C�������肷��ό`�͎��R�ɂł��܂��D �[���ł��Ȃ����́C(1)�̂悤�Ȏ����\�����e���Ɍ��ڍs�̑O�̒i�K�i�L���̒l����Ȃ鑝��Δx��Δy���琬��W�j =y �� =Δx �ōl���Ă݂�Ƃ悢.���̂悤�ɉ��߂���ΗL���̒lΔx��Δy���g���āu�P�Ȃ镪���v�Z�����Ă��邾���v�ɂȂ�C�|���Z�C����Z�Ȃǂ̕ό`�����R�ɂł��܂��D (2)�ɂ���
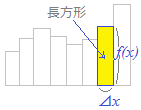
�@�T�d�ȕ��́C�Ȃ��ϕ��L����t������O������ł���̂��Ƌ^��Ɏv����������܂��C��ŏq�ׂ��悤�ɋɌ��ڍs����O�̒i�K�ōl�����
�X�̒����`�̖ʐς𑫂������\���Ă��邩��C�C�y�ɕt���邱�Ƃ��ł��܂��D (3)�ɂ���
�ϕ�����=log|x|+A�ɂ��܂��D
�Ō�ɔC�Ӓ萔�i�ϕ��萔�j�Ƃ���C���g�������̂ŁC�r���o�߂�A��B�܂���C1, C2�ōs���Ƃ悢�D (4)�ɂ���
�ΐ��̒�`�i�w���Ƒΐ��̊W�jar=M��r=logaM
���ɒꂪe�̏ꍇ�Cer=M��r=log M �ɂ��܂��D log|y|=x+A������|y|=ex+A�ɂȂ�܂��D ���ɁC�w���@��ap+q=apaq�ɂ�� ex+A=exeA �ɂȂ�܂��D |
||||||
|
�y��Q�z
�i����E�j����������=2xy�̈�ʉ������߂Ă��������D ���ӂ�dx���|���Cy�Ŋ����� =2xdx …(1) �ƕό`���܂��D  ���ӂ�ϕ������ =2xdx …(2)  log|y|=x2+A …(3)  |y|=ex2+A=eAex2 …(4)  eA��B(>0)�Ƃ����� |y|=Bex2  y=±Bex2  ±B��C(≠0)�Ƃ����� y=Cex2 (C≠0) …(5)
�i���Z�j
�ȏ�ɂ��Cy=Cex2 (C�͔C�ӂ̎���) …(��)(5)�����̔����������ɑ������ƁC �i���Ӂj=C2xex2=2x·Cex2=�i�E�Ӂj�ƂȂ��Đ�������D (5)�ɂ�����C=0�̂Ƃ���y=0�ƂȂ��āC���̏ꍇ�����̔��������������D�i���ى��ƌĂ��j |
�y��R�z
�i����E�j����������=�̈�ʉ������߂Ă��������D ���ӂ�dx���|���Cy�Ŋ����� = …(1) �ƕό`���܂��D  ���ӂ�ϕ������ = …(2)  log|y|=log|x|+A=log|x|+log eA=log eA|x| …(3) ���ӂ��P�̑ΐ��ɒ�����log|y|=log...�̌`�ɂ��邽�߂ɂ́CA→log eA�Ƃ���Ƃ悢
 |y|=eA|x| …(4)  eA��B(>0)�Ƃ����� |y|=B|x|  y=±Bx  ±B��C(≠0)�Ƃ����� y=Cx (C≠0) …(5)
�i���Z�j
�ȏ�ɂ��Cy=Cx (C�͔C�ӂ̎���) …(��)(5)�����̔����������ɑ������ƁC �i���Ӂj=C=�i�E�Ӂj�ƂȂ��Đ�������D (5)�ɂ�����C=0�̂Ƃ������̔��������������D �i���̔���������������ƌ��_(0, 0)�ɂ���������W������`����Ă��Ȃ����C�����������ň�����͔̂����\�Ȋ��ŁC���������ĘA���Ȋ��Ȃ̂ŁC���̕łł͂��̂悤�ȏ��O�_�̖��ɐ[���肵�Ȃ��D�j |
||||||
|
�y��S�z
�i����E�j����������(x+1)y’+(y−1)=0�̈�ʉ������߂Ă��������D �͂��߂�y’���ɒ����܂��D (x+1)+(y−1)=0 (x+1)=−(y−1) =− =− log|y−1|=−log|x+1|+A=−log|x+1|+log eA=log |y−1|= y−1=± ±eA��C(≠0)�Ƃ����� y−1= (C≠0) y=+1 (C≠0)
�i���Z�j
�ȏ�ɂ��Cy=+1 (C�͔C�ӂ̎���) …(��)y=+1�̂Ƃ� y−1=�Cy’=−������ �i���Ӂj=(x+1)(−)+=0 �ƂȂ��āC���̔��������������D
|
�y��T�z
�i����E�j����������=−�̈�ʉ������߂Ă��������D ydy=−xdx ydy=−xdx =−+A y2=−x2+2A y2+x2=2A 2A=C�Ƃ����� y2+x2=C
�i���Z�j
�ȏ�ɂ��Cy2+x2=C (C�͔C�ӂ̎���) …(��)y2+x2=C�̗��ӂ�x�Ŕ�������� (y2+x2)=(C) 2y+2x=0 y≠0�̂Ƃ� =− �ƂȂ��āC���̔��������������D �i�����������̉��́Cy�̗z���Fy=...�Ƃ����`��y�ɂ��ĉ����ꂽ�`�łȂ��Ă��悭�Cx=f(y)�̌`�ł��C�A��f(x, y)=...�̌`�ł��悢�D�j
|
||||||
|
�y���z
���̔����������̈�ʉ������߂Ă��������D���ى��͍l���Ȃ��Ă悢���̂Ƃ��C�͉E�̑I�����̔ԍ��œ����Ă��������D �i�r���o�߂͒����v�Z�ɂȂ�C�ÎZ�ł͖����ł��D�v�Z�p�����K�v�ł��D�j (1)y=Ce
=x2dx
=x2dx log|y|=+A |y|=e+A=eAe y=±eAe=Ce (2)y=Ce+x
=(x+1)dx
=(x+1)dx log|y|=+x+A |y|=e+x+A=eAe+x y=±eAe+x=Ce+x (3)y=log(ex+C)
=
eydy=exdx eydy=exdx ey=ex+C y=log(ex+C) |
��I������
1y=log(ex+C) 2y= 32x2+y2=C 4y=Ce+x 5y=C(x−1) 6y=Ce (4)2x2+y2=C
y+2x=0
y=−2x ydy=−2xdx ydy=−2xdx =−x2+A y2=−2x2+2A y2+2x2=2A y2+2x2=C (5)y=C(x−1)
(x−1)y’=y
(x−1)=y = = log|y|=log|x−1|+A=log|x−1|+log eA=log eA|x−1| |y|=eA|x−1| y=±eA(x−1)=C(x−1) |