|
���Z�`��w��b�̐��w�p��.����.��
�P�D�O�p���̏d�v�ȋɌ��l
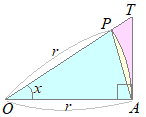
�@�O�p���̔����i�����j�����߂�Ƃ��C���̋Ɍ��l���d�v�ȓ��������܂��D�i���̋Ɍ����d�v�ł��闝�R1
�@(*1)�����߂邽�߂ɂ́C�O�p���̘a��ςɒ����������g���āC (�a��ςɒ�������) (*1)�� ���Ȃ킿�C �̋Ɍ��l���K�v�ɂȂ�܂��D |
���̋Ɍ����d�v�ł��闝�R2
�@(*2)�����߂邽�߂ɂ́C�O�p���̘a��ςɒ����������g���āC (�a��ςɒ�������) (*2)�� ���Ȃ킿�C �̋Ɍ��l���K�v�ɂȂ�܂��D ���R3
|
 �A�j
�A�j

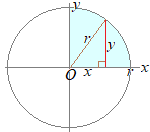 �@�܂��~�͏㉺���E�Ώ̂����礑�1�ی���4���~�ɂȂ�ʐς����߂āC���ʂ�4�{������߂���D
�@�܂��~�͏㉺���E�Ώ̂����礑�1�ی���4���~�ɂȂ�ʐς����߂āC���ʂ�4�{������߂���D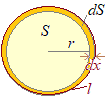 �@���a��
�@���a��